set of problem solving tools in mathematics

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

Free ready-to-use math resources

Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth

20 Effective Math Strategies To Approach Problem-Solving

Katie Keeton

Math strategies for problem-solving help students use a range of approaches to solve many different types of problems. It involves identifying the problem and carrying out a plan of action to find the answer to mathematical problems.

Problem-solving skills are essential to math in the general classroom and real-life. They require logical reasoning and critical thinking skills. Students must be equipped with strategies to help them find solutions to problems.

This article explores mathematical problem solving strategies, logical reasoning and critical thinking skills to help learners with solving math word problems independently in real-life situations.

What are problem-solving strategies?

Problem-solving strategies in math are methods students can use to figure out solutions to math problems. Some problem-solving strategies:

Draw a model
Use different approaches
Check the inverse to make sure the answer is correct

Students need to have a toolkit of math problem-solving strategies at their disposal to provide different ways to approach math problems. This makes it easier to find solutions and understand math better.

Strategies can help guide students to the solution when it is difficult ot know when to start.

The ultimate guide to problem solving techniques

Download these ready-to-go problem solving techniques that every student should know. Includes printable tasks for students including challenges, short explanations for teachers with questioning prompts.

20 Math Strategies For Problem-Solving

Different problem-solving math strategies are required for different parts of the problem. It is unlikely that students will use the same strategy to understand and solve the problem.

Here are 20 strategies to help students develop their problem-solving skills.

Strategies to understand the problem

Strategies that help students understand the problem before solving it helps ensure they understand:

The context
What the key information is
How to form a plan to solve it

Following these steps leads students to the correct solution and makes the math word problem easier .

Here are five strategies to help students understand the content of the problem and identify key information.

1. Read the problem aloud

Read a word problem aloud to help understand it. Hearing the words engages auditory processing. This can make it easier to process and comprehend the context of the situation.

2. Highlight keywords

When keywords are highlighted in a word problem, it helps the student focus on the essential information needed to solve it. Some important keywords help determine which operation is needed. For example, if the word problem asks how many are left, the problem likely requires subtraction. Ensure students highlight the keywords carefully and do not highlight every number or keyword. There is likely irrelevant information in the word problem.

3. Summarize the information

Read the problem aloud, highlight the key information and then summarize the information. Students can do this in their heads or write down a quick summary. Summaries should include only the important information and be in simple terms that help contextualize the problem.

4. Determine the unknown

A common problem that students have when solving a word problem is misunderstanding what they are solving. Determine what the unknown information is before finding the answer. Often, a word problem contains a question where you can find the unknown information you need to solve. For example, in the question ‘How many apples are left?’ students need to find the number of apples left over.

5. Make a plan

Once students understand the context of the word problem, have dentified the important information and determined the unknown, they can make a plan to solve it. The plan will depend on the type of problem. Some problems involve more than one step to solve them as some require more than one answer. Encourage students to make a list of each step they need to take to solve the problem before getting started.

Strategies for solving the problem

1. draw a model or diagram.

Students may find it useful to draw a model, picture, diagram, or other visual aid to help with the problem solving process. It can help to visualize the problem to understand the relationships between the numbers in the problem. In turn, this helps students see the solution.

math problem that needs a problem solving strategy

Similarly, you could draw a model to represent the objects in the problem:

2. Act it out

This particular strategy is applicable at any grade level but is especially helpful in math investigation in elementary school . It involves a physical demonstration or students acting out the problem using movements, concrete resources and math manipulatives . When students act out a problem, they can visualize and contectualize the word problem in another way and secure an understanding of the math concepts. The examples below show how 1st-grade students could “act out” an addition and subtraction problem:

3. Work backwards

Working backwards is a popular problem-solving strategy. It involves starting with a possible solution and deciding what steps to take to arrive at that solution. This strategy can be particularly helpful when students solve math word problems involving multiple steps. They can start at the end and think carefully about each step taken as opposed to jumping to the end of the problem and missing steps in between.

For example,

To solve this problem working backwards, start with the final condition, which is Sam’s grandmother’s age (71) and work backwards to find Sam’s age. Subtract 20 from the grandmother’s age, which is 71. Then, divide the result by 3 to get Sam’s age. 71 – 20 = 51 51 ÷ 3 = 17 Sam is 17 years old.

4. Write a number sentence

When faced with a word problem, encourage students to write a number sentence based on the information. This helps translate the information in the word problem into a math equation or expression, which is more easily solved. It is important to fully understand the context of the word problem and what students need to solve before writing an equation to represent it.

5. Use a formula

Specific formulas help solve many math problems. For example, if a problem asks students to find the area of a rug, they would use the area formula (area = length × width) to solve. Make sure students know the important mathematical formulas they will need in tests and real-life. It can help to display these around the classroom or, for those who need more support, on students’ desks.

Strategies for checking the solution

Once the problem is solved using an appropriate strategy, it is equally important to check the solution to ensure it is correct and makes sense.

There are many strategies to check the solution. The strategy for a specific problem is dependent on the problem type and math content involved.

Here are five strategies to help students check their solutions.

1. Use the Inverse Operation

For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7. As good practice, encourage students to use the inverse operation routinely to check their work.

2. Estimate to check for reasonableness

Once students reach an answer, they can use estimation or rounding to see if the answer is reasonable. Round each number in the equation to a number that’s close and easy to work with, usually a multiple of ten. For example, if the question was 216 ÷ 18 and the quotient was 12, students might round 216 to 200 and round 18 to 20. Then use mental math to solve 200 ÷ 20, which is 10. When the estimate is clear the two numbers are close. This means your answer is reasonable.

3. Plug-In Method

This method is particularly useful for algebraic equations. Specifically when working with variables. To use the plug-in method, students solve the problem as asked and arrive at an answer. They can then plug the answer into the original equation to see if it works. If it does, the answer is correct.

If students use the equation 20m+80=300 to solve this problem and find that m = 11, they can plug that value back into the equation to see if it is correct. 20m + 80 = 300 20 (11) + 80 = 300 220 + 80 = 300 300 = 300 ✓

4. Peer Review

Peer review is a great tool to use at any grade level as it promotes critical thinking and collaboration between students. The reviewers can look at the problem from a different view as they check to see if the problem was solved correctly. Problem solvers receive immediate feedback and the opportunity to discuss their thinking with their peers. This strategy is effective with mixed-ability partners or similar-ability partners. In mixed-ability groups, the partner with stronger skills provides guidance and support to the partner with weaker skills, while reinforcing their own understanding of the content and communication skills. If partners have comparable ability levels and problem-solving skills, they may find that they approach problems differently or have unique insights to offer each other about the problem-solving process.

5. Use a Calculator

A calculator can be introduced at any grade level but may be best for older students who already have a foundational understanding of basic math operations. Provide students with a calculator to allow them to check their solutions independently, accurately, and quickly. Since calculators are so readily available on smartphones and tablets, they allow students to develop practical skills that apply to real-world situations.

Step-by-step problem-solving processes for your classroom

In his book, How to Solve It , published in 1945, mathematician George Polya introduced a 4-step process to solve problems.

Polya’s 4 steps include:

Understand the problem
Devise a plan
Carry out the plan

Today, in the style of George Polya, many problem-solving strategies use various acronyms and steps to help students recall.

Many teachers create posters and anchor charts of their chosen process to display in their classrooms. They can be implemented in any elementary, middle school or high school classroom.

Here are 5 problem-solving strategies to introduce to students and use in the classroom.

How Third Space Learning improves problem-solving

Resources .

Third Space Learning offers a free resource library is filled with hundreds of high-quality resources. A team of experienced math experts carefully created each resource to develop students mental arithmetic, problem solving and critical thinking.

Explore the range of problem solving resources for 2nd to 8th grade students.

One-on-one tutoring

Third Space Learning offers one-on-one math tutoring to help students improve their math skills. Highly qualified tutors deliver high-quality lessons aligned to state standards.

Former teachers and math experts write all of Third Space Learning’s tutoring lessons. Expertly designed lessons follow a “my turn, follow me, your turn” pedagogy to help students move from guided instruction and problem-solving to independent practice.

Throughout each lesson, tutors ask higher-level thinking questions to promote critical thinking and ensure students are developing a deep understanding of the content and problem-solving skills.

Problem-solving

Educators can use many different strategies to teach problem-solving and help students develop and carry out a plan when solving math problems. Incorporate these math strategies into any math program and use them with a variety of math concepts, from whole numbers and fractions to algebra.

Teaching students how to choose and implement problem-solving strategies helps them develop mathematical reasoning skills and critical thinking they can apply to real-life problem-solving.

Ultimate Guide to Metacognition [FREE]

Looking for a summary on metacognition in relation to math teaching and learning?

Check out this guide featuring practical examples, tips and strategies to successfully embed metacognition across your school to accelerate math growth.

Privacy Overview

Math Solver

Geogebra math solver.

Get accurate solutions and step-by-step explanations for algebra and other math problems, while enhancing your problem-solving skills!

person with long dark hair sit at a table working at a laptop. 3x+2 and x² equations float in the air signifying that she is working on math problems

Get step-by-step solutions to your math problems

$qr code$

Try Math Solver

Get step-by-step explanations

$Graph your math problems$

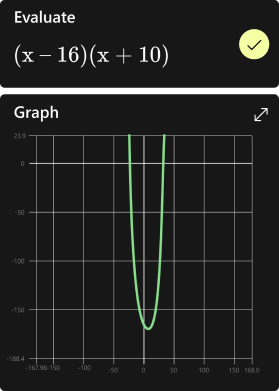
Graph your math problems

$Practice, practice, practice$

Practice, practice, practice

$Get math help in your language$

Solver Title

Generating PDF...

Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
Linear Algebra Matrices Vectors
Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
Physics Mechanics
Chemistry Chemical Reactions Chemical Properties
Finance Simple Interest Compound Interest Present Value Future Value
Economics Point of Diminishing Return
Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
Pre Algebra
Pre Calculus
Linear Algebra
Trigonometry
Conversions

Most Used Actions

Number line.

x^{2}-x-6=0
-x+3\gt 2x+1
line\:(1,\:2),\:(3,\:1)
prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
\frac{d}{dx}(\frac{3x+9}{2-x})
(\sin^2(\theta))'
\lim _{x\to 0}(x\ln (x))
\int e^x\cos (x)dx
\int_{0}^{\pi}\sin(x)dx
\sum_{n=0}^{\infty}\frac{3}{2^n}
Is there a step by step calculator for math?
Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
Is there a step by step calculator for physics?
Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
How to solve math problems step-by-step?
To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
My Notebook, the Symbolab way Math notebooks have been around for hundreds of years. You write down problems, solutions and notes to go back...

Please add a message.

Message received. Thanks for the feedback.

Solve equations and inequalities
Simplify expressions
Factor polynomials
Graph equations and inequalities
Advanced solvers
All solvers
Arithmetics
Determinant
Percentages
Scientific Notation
Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
The calculus section will carry out differentiation as well as definite and indefinite integration.
The matrices section contains commands for the arithmetic manipulation of matrices.
The graphs section contains commands for plotting equations and inequalities.
The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

Add Fractions
Simplify Fractions

Mathematics as a Complex Problem-Solving Activity

By jacob klerlein and sheena hervey, generation ready.

By the time young children enter school they are already well along the pathway to becoming problem solvers. From birth, children are learning how to learn: they respond to their environment and the reactions of others. This making sense of experience is an ongoing, recursive process. We have known for a long time that reading is a complex problem-solving activity. More recently, teachers have come to understand that becoming mathematically literate is also a complex problem-solving activity that increases in power and flexibility when practiced more often. A problem in mathematics is any situation that must be resolved using mathematical tools but for which there is no immediately obvious strategy. If the way forward is obvious, it’s not a problem—it is a straightforward application.

Mathematicians have always understood that problem-solving is central to their discipline because without a problem there is no mathematics. Problem-solving has played a central role in the thinking of educational theorists ever since the publication of Pólya’s book “How to Solve It,” in 1945. The National Council of Teachers of Mathematics (NCTM) has been consistently advocating for problem-solving for nearly 40 years, while international trends in mathematics teaching have shown an increased focus on problem-solving and mathematical modeling beginning in the early 1990s. As educators internationally became increasingly aware that providing problem-solving experiences is critical if students are to be able to use and apply mathematical knowledge in meaningful ways (Wu and Zhang 2006) little changed at the school level in the United States.

“Problem-solving is not only a goal of learning mathematics, but also a major means of doing so.”

(NCTM, 2000, p. 52)

In 2011 the Common Core State Standards incorporated the NCTM Process Standards of problem-solving, reasoning and proof, communication, representation, and connections into the Standards for Mathematical Practice. For many teachers of mathematics this was the first time they had been expected to incorporate student collaboration and discourse with problem-solving. This practice requires teaching in profoundly different ways as schools moved from a teacher-directed to a more dialogic approach to teaching and learning. The challenge for teachers is to teach students not only to solve problems but also to learn about mathematics through problem-solving. While many students may develop procedural fluency, they often lack the deep conceptual understanding necessary to solve new problems or make connections between mathematical ideas.

“A problem-solving curriculum, however, requires a different role from the teacher. Rather than directing a lesson, the teacher needs to provide time for students to grapple with problems, search for strategies and solutions on their own, and learn to evaluate their own results. Although the teacher needs to be very much present, the primary focus in the class needs to be on the students’ thinking processes.”

(Burns, 2000, p. 29)

Learning to problem solve

To understand how students become problem solvers we need to look at the theories that underpin learning in mathematics. These include recognition of the developmental aspects of learning and the essential fact that students actively engage in learning mathematics through “doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning” (Copley, 2000, p. 29). The concept of co-construction of learning is the basis for the theory. Moreover, we know that each student is on their unique path of development.

Beliefs underpinning effective teaching of mathematics

Every student’s identity, language, and culture need to be respected and valued.
Every student has the right to access effective mathematics education.
Every student can become a successful learner of mathematics.

Children arrive at school with intuitive mathematical understandings. A teacher needs to connect with and build on those understandings through experiences that allow students to explore mathematics and to communicate their ideas in a meaningful dialogue with the teacher and their peers.

Learning takes place within social settings (Vygotsky, 1978). Students construct understandings through engagement with problems and interaction with others in these activities. Through these social interactions, students feel that they can take risks, try new strategies, and give and receive feedback. They learn cooperatively as they share a range of points of view or discuss ways of solving a problem. It is through talking about problems and discussing their ideas that children construct knowledge and acquire the language to make sense of experiences.

Students acquire their understanding of mathematics and develop problem-solving skills as a result of solving problems, rather than being taught something directly (Hiebert1997). The teacher’s role is to construct problems and present situations that provide a forum in which problem-solving can occur.

Why is problem-solving important?

Our students live in an information and technology-based society where they need to be able to think critically about complex issues, and “analyze and think logically about new situations, devise unspecified solution procedures, and communicate their solution clearly and convincingly to others” (Baroody, 1998). Mathematics education is important not only because of the “gatekeeping role that mathematics plays in students’ access to educational and economic opportunities,” but also because the problem-solving processes and the acquisition of problem-solving strategies equips students for life beyond school (Cobb, & Hodge, 2002).

The importance of problem-solving in learning mathematics comes from the belief that mathematics is primarily about reasoning, not memorization. Problem-solving allows students to develop understanding and explain the processes used to arrive at solutions, rather than remembering and applying a set of procedures. It is through problem-solving that students develop a deeper understanding of mathematical concepts, become more engaged, and appreciate the relevance and usefulness of mathematics (Wu and Zhang 2006). Problem-solving in mathematics supports the development of:

The ability to think creatively, critically, and logically
The ability to structure and organize
The ability to process information
Enjoyment of an intellectual challenge
The skills to solve problems that help them to investigate and understand the world

Problem-solving should underlie all aspects of mathematics teaching in order to give students the experience of the power of mathematics in the world around them. This method allows students to see problem-solving as a vehicle to construct, evaluate, and refine their theories about mathematics and the theories of others.

Problems that are “Problematic”

The teacher’s expectations of the students are essential. Students only learn to handle complex problems by being exposed to them. Students need to have opportunities to work on complex tasks rather than a series of simple tasks devolved from a complex task. This is important for stimulating the students’ mathematical reasoning and building durable mathematical knowledge (Anthony and Walshaw, 2007). The challenge for teachers is ensuring the problems they set are designed to support mathematics learning and are appropriate and challenging for all students. The problems need to be difficult enough to provide a challenge but not so difficult that students can’t succeed. Teachers who get this right create resilient problem solvers who know that with perseverance they can succeed. Problems need to be within the students’ “Zone of Proximal Development” (Vygotsky 1968). These types of complex problems will provide opportunities for discussion and learning.

Students will have opportunities to explain their ideas, respond to the ideas of others, and challenge their thinking. Those students who think math is all about the “correct” answer will need support and encouragement to take risks. Tolerance of difficulty is essential in a problem-solving disposition because being “stuck” is an inevitable stage in resolving just about any problem. Getting unstuck typically takes time and involves trying a variety of approaches. Students need to learn this experientially. Effective problems:

Are accessible and extendable
Allow individuals to make decisions
Promote discussion and communication
Encourage originality and invention
Encourage “what if?” and “what if not?” questions
Contain an element of surprise (Adapted from Ahmed, 1987)

“Students learn to problem solve in mathematics primarily through ‘doing, talking, reflecting, discussing, observing, investigating, listening, and reasoning.”

(Copley, 2000, p. 29)

“…as learners investigate together. It becomes a mini- society – a community of learners engaged in mathematical activity, discourse and reflection. Learners must be given the opportunity to act as mathematicians by allowing, supporting and challenging their ‘mathematizing’ of particular situations. The community provides an environment in which individual mathematical ideas can be expressed and tested against others’ ideas.…This enables learners to become clearer and more confident about what they know and understand.”

(Fosnot, 2005, p. 10)

Research shows that ‘classrooms where the orientation consistently defines task outcomes in terms of the answers rather than the thinking processes entailed in reaching the answers negatively affects the thinking processes and mathematical identities of learners’ (Anthony and Walshaw, 2007, page 122).

Effective teachers model good problem-solving habits for their students. Their questions are designed to help children use a variety of strategies and materials to solve problems. Students often want to begin without a plan in mind. Through appropriate questions, the teacher gives students some structure for beginning the problem without telling them exactly what to do. In 1945 Pólya published the following four principles of problem-solving to support teachers with helping their students.

Understand and explore the problem
Find a strategy
Use the strategy to solve the problem
Look back and reflect on the solution

Problem-solving is not linear but rather a complex, interactive process. Students move backward and forward between and across Pólya’s phases. The Common Core State Standards describe the process as follows:

“Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary”. (New York State Next Generation Mathematics Learning Standards 2017).

Pólya’s Principals of Problem-Solving

Polyas principles of problem solving graphic

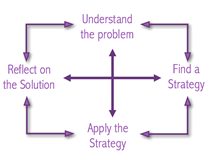
Students move forward and backward as they move through the problem-solving process.

The goal is for students to have a range of strategies they use to solve problems and understand that there may be more than one solution. It is important to realize that the process is just as important, if not more important, than arriving at a solution, for it is in the solution process that students uncover the mathematics. Arriving at an answer isn’t the end of the process. Reflecting on the strategies used to solve the problem provides additional learning experiences. Studying the approach used for one problem helps students become more comfortable with using that strategy in a variety of other situations.

When making sense of ideas, students need opportunities to work both independently and collaboratively. There will be times when students need to be able to work independently and other times when they will need to be able to work in small groups so that they can share ideas and learn with and from others.

Getting real

Effective teachers of mathematics create purposeful learning experiences for students through solving problems in relevant and meaningful contexts. While word problems are a way of putting mathematics into contexts, it doesn’t automatically make them real. The challenge for teachers is to provide students with problems that draw on their experience of reality, rather than asking them to suspend it. Realistic does not mean that problems necessarily involve real contexts, but rather they make students think in “real” ways.

Planning for talk

By planning for and promoting discourse, teachers can actively engage students in mathematical thinking. In discourse-rich mathematics classes, students explain and discuss the strategies and processes they use in solving mathematical problems, thereby connecting their everyday language with the specialized vocabulary of mathematics.

Students need to understand how to communicate mathematically, give sound mathematical explanations, and justify their solutions. Effective teachers encourage their students to communicate their ideas orally, in writing, and by using a variety of representations. Through listening to students, teachers can better understand what their students know and misconceptions they may have. It is the misconceptions that provide a window into the students’ learning process. Effective teachers view thinking as “the process of understanding,” they can use their students’ thinking as a resource for further learning. Such teachers are responsive both to their students and to the discipline of mathematics.

“Mathematics today requires not only computational skills but also the ability to think and reason mathematically in order to solve the new problems and learn the new ideas that students will face in the future. Learning is enhanced in classrooms where students are required to evaluate their own ideas and those of others, are encouraged to make mathematical conjectures and test them, and are helped to develop their reasoning skills.”

(John Van De Walle)

“Equity. Excellence in mathematics education requires equity—high expectations and strong support for all students.”

How teachers organize classroom instruction is very much dependent on what they know and believe about mathematics and on what they understand about mathematics teaching and learning. Teachers need to recognize that problem-solving processes develop over time and are significantly improved by effective teaching practices. The teacher’s role begins with selecting rich problem-solving tasks that focus on the mathematics the teacher wants their students to explore. A problem-solving approach is not only a way for developing students’ thinking, but it also provides a context for learning mathematical concepts. Problem-solving allows students to transfer what they have already learned to unfamiliar situations. A problem-solving approach provides a way for students to actively construct their ideas about mathematics and to take responsibility for their learning. The challenge for mathematics teachers is to develop the students’ mathematical thinking process alongside the knowledge and to create opportunities to present even routine mathematics tasks in problem-solving contexts.

Given the efforts to date to include problem-solving as an integral component of the mathematics curriculum and the limited implementation in classrooms, it will take more than rhetoric to achieve this goal. While providing valuable professional learning, resources, and more time are essential steps, it is possible that problem-solving in mathematics will only become valued when high-stakes assessment reflects the importance of students’ solving of complex problems.

Trending Now
Foundational Courses
Data Science
Practice Problem
Machine Learning
System Design
DevOps Tutorial
10 Best AI Tools to Boost Productivity in 2024
10 Best ChatGPT Prompts to Solve Complex Math Problems
How to Use Algorithms to Solve Problems?
How to use Chat-GPT to solve Coding Problems?
Top 12 AI Tools for Remote Learning and Online Education
12 Best AI Tools for People with Disabilities [Latest 2024]
7 Best AI Tools for Healthcare Professionals free in 2024
What are Mathematical Puzzles and How to solve them?
7 AI Tools You Can Use to Make Money Online
Top 10 AI Poster Making Tools To Be Used in 2024
10 Best AI Tools for Lawyers (Free + Paid)
7 Best AI Tools for IT Professionals (2024)
Top 15 Artificial Intelligence(AI) Tools List
10 Best AI SEO Tools to Boost Your Rankings in 2024
10 Best AI Search Engines To Try in 2024
Problems on Ages - Aptitude Questions and Answers
Top 12 AI Testing Tools for Test Automation in 2024
Reasoning Tricks to Solve Coding -Decoding and Calendar Problems
10 AI Tools Under US $10 Per Month Worth Investing

10 Best Math AI Solvers to Solve Math Problems Online

Tackling challenging math problems can be a time-consuming endeavor. Math AI solvers make learning math simple. These AI-powered tools use machine learning and advanced algorithms to rapidly analyze math problems at all grade levels. Whether you’re a high school student or at the college level, an AI math problem solver can help save you time, ensure accuracy, and boost your school success.

With 24/7 convenience, they can be used anytime to get instant help with confusing math problems. When curating our list of top 10 best math AI solvers, we looked at several important factors, such as pricing, features, strengths, and weaknesses. Let’s explore these tools and learn in which areas they excel:

Mathful – Best Overall Math AI Solver to Solve Math Problems

Mathful is a valuable AI math solver often used by students to get help with complicated math problems. It delivers step-by-step guidance that breaks down the problem to make it easier to digest. The tool also provides the final answer to allow students to verify their solutions and gain confidence in their math skills.

Mathful is available 24/7, making it a convenient tool for students to get instant help with their math homework. Mathful acts as the ultimate solution for boosting academic success at all math levels.

Helps students gain a deeper understanding of math concepts with step-by-step guidance.
Serves as a verification tool where students can check their work without costing a dime.
Enables students to complete their math homework with just one click.
Cannot be used to supplement a real classroom education.

Solve Math Problems Instantly with Mathful’s AI Math Solver >>>

AI Math – Best AI Math Solver for All Grade Levels

$AI-Math$

AI Math is an innovative math AI solver designed to solve a wide range of mathematical problems, ranging from basic math concepts to more challenging equations.

The way this unique tool works is by analyzing the math problem, finding potential solutions, validating those solutions, and returning the best possible results for the given problem.

While some math AI tools are only capable of solving basic math problems, AI Math is more diverse. Use it to solve math problems at all grade levels, from elementary to university and beyond. AI Math is trained on an extensive database of mathematical information and can guarantee 98% accuracy.

Generates solutions to math problems with a high rate of accuracy.
Designed to provide almost instant results for efficiency.
Covers all types of math and homework at all grade levels.
Requires a subscription after the initial trial period.

HIX Tutor – Best AI Math Solver for High Accuracy

HIX Tutor provides students with the solutions they need to understand and solve their math problems.

With this powerful math solver AI tool, users can type in a math question or upload a document or image of the question. Using this input, Math AI Solver uses machine learning technology to perform dynamic calculations and give users the correct answer.

HIX Tutor can provide solutions for math homework problems at all levels with a 98% accuracy rate. However, the tool goes beyond mere problem-solving by offering comprehensive calculations on how to solve the problem from start to finish.

Provides step-by-step solutions to math problems.
Is less expensive than hiring a math tutor.
Can type in math questions or upload documents or images of the problem.
May have difficulty recognizing documents with messy handwriting.

HomeworkAI – Best All-in-One Solution for Homework Help

HomeworkAI is the ultimate homework assistant that can be used to get answers to any homework question, from math and science to history and geography. Its math AI solver acts as your personal AI tutor by providing comprehensive solutions to math problems that help students better understand the material.

This unique AI tool is available 24/7, making it a convenient and accessible resource for students who need immediate help with their homework. As the tool is free to try, students can get started right away by asking a math question that they’re struggling with. HomeworkAI can also help students prepare for important tests or exams by providing step-by-step instructions on how to work through certain math questions.

Covers all school subjects, including math.
Provides step-by-step explanations for each math problem.
Supports multiple math problem input methods.
Some math solutions may be difficult to understand.

Question AI – Best Homework AI Tool for Greater Academic Success

Question AI is a leading homework helper that uses powerful AI technology to instantly help with any school subject. Question AI is often used for any math problems, covering algebra, geometry, calculus, arithmetic, and trigonometry. Students often waste hours struggling with challenging homework questions they simply don’t understand. Question AI simplifies the homework process by breaking down the question to make it easier to learn. The math AI solver also promises a 99% accurate answer to the math question, allowing students to verify their own work.

Question AI serves as an innovative all-in-one product for AI homework help. It is a highly effective tool for helping students reach greater academic achievement.

Covers all homework subjects, including all branches of mathematics.
Boosts student grades.
Supports many different languages.
Accuracy may be limited beyond core math subjects.
The mobile app is not yet available.
Costs money after the free trial.

QuickMath – Best Math AI Solver for High School and College Students

$Quick-Math$

QuickMath is designed to automatically answer common math problems in algebra, calculus, and equations. The tool offers several options for solving math problems, including solving an equation, inequality, or a system. It can also simplify an expression, factor an expression, or expand a product or power. The diverse AI math solver can also graph, find the greatest common factor, and the least common measure. Advanced math solvers are also available for more complex math problems.

QuickMath is geared toward high school and college-level students. The tool’s features and capabilities are always being improved to ensure that users have access to the most comprehensive AI math tools available.

Offers a wide range of standard and advanced math solvers.
Available to download on the App Store and Google Play.
Quick-solve tutorials are available to help users learn math concepts.
Math problems must be typed in and cannot be uploaded.
Not suitable for grade levels lower than high school.
Some users may receive Timeout messages due to 15-second CPU time rules.

Smodin – Best AI Math Solver for Acing Math Exams

Smodin Math AI Homework Solver offers a fast and effective way to prepare for difficult math exams. The versatile homework helper uses machine learning and advanced algorithms to help students learn core math concepts and boost their grades in school. Simply input a question or assignment and Smodin instantly generates step-by-step solutions. The math solver AI tool consists of a simple interface that allows students to enter a question to solve. At the click of a button, the tool starts working to analyze the problem and present the best answer based on the equation.

While Smodin Math AI Homework Solver does lack advanced features and capabilities, it can be a useful tool for students who want to study before a big math test.

Provides in-depth answers to math questions to help students ace math exams.
Users are given 3 free credits a day to ask math questions.
The clean interface makes it easy to enter math questions to solve.
Offers no advanced math features or capabilities.
Users must pay for a subscription after reaching the daily credit limit.

StudyMonkey – Best AI Math Problem Solver for Personalized Learning

StudyMonkey is a diverse homework helper for students that uses complex machine learning capabilities to provide step-by-step guidance on many school subjects, including math. The innovative math AI solver can be used by learners of all backgrounds and ages to improve their understanding of math concepts and enhance their academic success. With round-the-clock availability, this unique tool can save students significant time when completing homework assignments.

Students can personalize their output based on the subject and grade level.
There is a free plan for users that only requires occasional homework help.
Users can see a history of past questions and answers.
Users must purchase a paid plan to ask more than 3 questions daily.
Answers to more complex math questions may not be as accurate.
Must upgrade to the $8 plan to use the Advanced AI Model.

Interactive Mathematics – Best Math AI Tool for Solving Word Problems

Interactive Mathematics claims to be more accurate than ChatGPT, faster than a math tutor, and more powerful than a math calculator. The advanced AI math problem solver has been trained in a wide array of math subjects, such as basic algebra, advanced algebra, trigonometry, geometry, calculus, advanced calculus, physics, and more. It is also highly effective at solving math word problems with step-by-step solutions.

With Interactive Mathematics, users can type in their math problems or copy and paste a photo. The tool then analyzes the problem and delivers near-instant results.

Efficient at solving math word problems.
Optimized for mobile phones and tablet use.
A subscription comes with additional discounts and bonuses.
Users can only ask 3 questions before having to upgrade to the paid version.
No app is yet available.
Pushes tutoring services when the tool is unable to give an accurate answer.

SnapXam – Best AI Math Solver for On-the-Go

SnapXam is an AI-powered math tutor that can help students better understand different types of math, from calculus to trigonometry. After entering the math problem, the tool quickly presents the final answer, as well as a step-by-step solution that shows how to work out the problem.

The unique AI math problem solver also provides access to informative YouTube videos that students can watch to learn more about different concepts in math.

Upgrading to a Premium account can give students access to even more features and perks, including no ads, support for more than 100 math topics, and premium access to the iOS and Android apps.

Students can get AI math help with only access to a smartphone.
Offers multiple solving methods.
Covers more than 100 different math topics.
An ad-free environment is only available with the premium version.
Geared toward older students.
Accuracy issues may occur with advanced math problems.

Completing math assignments can be a long and tedious process. Having access to the best math AI tools can help eliminate the stress and frustration that come with not understanding math problems. For convenience, efficiency, and unmatched accuracy, try some of the top math AI tools like Mathful for free today!

This is a guest post, created for informational purposes only, and should not be considered as professional advice. Readers are encouraged to conduct their own research and consult with relevant experts before making any financial or investment decisions.

Please Login to comment...

Similar reads, improve your coding skills with practice.

What kind of Experience do you want to share?

Educational Software /
Learning Management Software (LMS) /

List of Top 13 Math Software to Solve Math Problem Efficiently

Table of Contents

9 Open Source Intelligence Tools and Techniques (OSINT Tools)
Latest Best Free Parental Control App for Android & iPhone
Top 7 FRP Bypass Tools Free for PC
How PLM Software Improves Product Engineering Management for eCommerce
How to Optimize Product Growth & Maturity with Siemens Teamcenter

List of Top 13 Math Software to Solve Math Problem Efficiently-feature image

Solving math problems has often been stressful for students, engineers, and teachers. However, there are few math software that helps solve and explain complex mathematical equations accurately and efficiently.

There are dozens of Math problem solving programs available online with different specializations and problem-solving abilities. This article will provide you with a list of the top 13 math software that solves math queries efficiently.

Best Math Software for Teachers, Students, and Engineers

Microsoft math solver, khan academy.

We have compiled some of the best math problem solving websites and software for you.

Best Math Software for Students

Students prefer online math software that not only provides accurate answers but also includes step by step guide to the answer. Here are our top choices for math software online .

$Microsoft Math Solver$

Microsoft Math Solver is simple yet powerful math problem solving application available for free on the Microsoft Store. It can be used by students of all levels, from elementary to college.

Microsoft Math Solver Features

Complex Graphing Calculator 
Step-by-step guide builder
Practice question sets
Multiple Languages including Hindi
Powerful scanning and solving
Sketch Calculator

Microsoft Mathematics Pricing: Microsoft Math Solver is a free software for mathematics.

Microsoft Math Solver Compatibility: Users can download and install it in Windows 8 and above. Besides, you can also use the math software online through Edge browser.

Suggested Read: Fun and Educational Best Software for Kids between Age 4-15+

GeoGebra is an open-source software for math calculation, popular among teachers and students due to its interactive learning feature.

The platform supports various mathematical concepts such as geometry, algebra, and calculus and provides different module for each function. It could also be accessed directly via web for online math problem solving.

GeoGebra Features

Create interactive geometric constructions
Quick Graphing Calculator
Interactive learning sessions
CAS and 3D Calculator
Collaborative Whiteboard
Perform statistical analyses
Data Visualization in dynamic graphs

GeoGebra Pricing: GeoGebra is an open-source math software available for free.

GeoGebra Compatibility: Available for Windows, macOS, Linux, Chromebook, and Linux. GeoGebra mobile apps for iOS and Android devices.

Mathway is an online math problem-solving software that offers step by step guide on how to solve a particular math problem. You cannot only find the answer to a specific problem but also determine the way of solving the question.

Mathway Features:

Method Selection
Precalculus problem solver
Graphical representation
Powerful statistical calculation

Mathway Pricing: It is a completely free online math problem solver for both students and teachers.

Mathway Compatibility: It is web-based software and can be used from any device through the web browser.

Suggested Read: Trending Learning Apps for Kids – Best Education Apps for Growing Kids

Photomath is one of the best math problem-solving software for parents, teachers, and students. It’s extremely simple user interface and easy navigation help users to quickly solve any math queries.

Besides students can also use the camera of their mobile device to click and scan a particular math problem. It provides step by step guide to solve it.

Photomath Features:

Point and Click Camera Calculator
Instant scan and Solve Math Problems
Focused process explanations
Personalized Visual Aids
Shared core-alignment
Deep solution extractor

Photomath Pricing: Photomath is a free math solver app available for iOS and Android devices. The premium Photomath Plus plan starts at Rs 387.20/ month with advanced features.

Photomath Compatibility: It is compatible with all Android and iOS devices.

Best Math Software for Teachers

Some math software is designed to help teachers by giving step-by-step solutions to high school or college mathematics problems. These are some of the best online math problem-solving websites that help teachers and professors.

Khan Academy is an ed-tech platform that provides multiple tools to teachers including a large database for math problem solving. It is designed to help teachers with planning and delivering math lessons, as well as assessing student progress.

Khan Academy Features:

Lesson builder
Progress tracker
Huge Resource Pool 
Grade-wise problem bifurcation

Khan Academy App Pricing: Khan Academy is a nonprofit Ed-tech platform. Anyone can study or contribute to the platform for free.

Khan Academy App Compatibility: Khan Academy app is available for both Android and iOS devices. Users can also log in through web browsers.

Suggested Read: Top Online Student Database Management System

QuickMath is another extremely powerful math software on this list specially designed for teachers and students. It allows users to quickly find answers to complicated math problems within a few steps. It also provides multiple formats making it easy for teachers to input algebraic and polynomial expressions.

Quickmath Features:

Inbuilt Advanced Solvers
Example based structuring
Automated Correction
Graphing, equation, and inequalities

QuickMath Pricing: QuickMath is a completely free online math problem solver.

QuickMmath Compatibility: QuickMath is available on both Apple Store and Play store for smartphones. Besides, it could also be used through the web.

Cymath is another powerful math problem-solving software for teachers. It not only provides a step-by-step solution to any problem but also explains every step for logical understanding of a Math concept.

Cymath Features:

Powerful Search feature
Online Equation Solver
Graphing Tools
Wide Range of Mathematical Functions
Reference material learning

Cymath Pricing: Cymath offers a free basic plan with limited features. The premium plan starts at around Rs 400/month with advanced features.

Cymath Compatibility: Cymath is an online math problem-solving website that can be accessed through a browser. It is also available for both Android and iOS devices.

Suggested Read: What is the Purpose of Student Information Systems? Evaluating Best Examples

Open Source and Free Math Software

While academic mathematics is simple, engineering and research level maths are complex. Due to these reasons, engineers, scientists and researchers need open source and free math problem-solving software. Here are three top open source and free software for math problems.

$Scilab math software$

Scilab is a free and open-source math problem-solving software for numerical computation. It provides an interactive environment to perform matrix operations, plot functions, and write algorithms.

Moreover, this free Math software also offers various toolboxes for specific purposes such as statistics, optimization, and signal processing.

Scilab Free Math Software Features:

High-level language for technical computation
Numerical analysis with a huge library of mathematical functions
Interface with C/C++, Fortran, Java, Python, and more
2D & 3D graphical representations of data
Textual and visual programming interface

Scilab Pricing: Scilab is opens source and free math software for engineers and researchers.

Compatibility: Scilab is compatible for Windows, macOS and Linux operating system.

GAP is an open-source system for computational discrete algebra with particular emphasis on computational group theory. GAP has powerful programming language including a library of thousands of functions implementing algebraic algorithms written in the GAP language.

GAP Features:

The inbuilt data type for major algebraic objects
Automated method selection
Pascal-like structure control
Automate garbage and memory management
Profiling and debugging facilities

GAP Pricing: GAP is completely free and open-source math software. Anyone can download and modify the application for non-commercial use.

GAP Free Math Software Compatibility: GAP could be installed in Linux, UNIX, or macOS.

Suggested Read: Best Learning Management Systems (LMS)

Gretl is a free and open-source cross-platform math and statistical package for econometric analysis. Gretl supports numerous linear and nonlinear statistical models, including OLS, 2SLS, GARCH, and so on.

Gretl Free Math Software Features:

MPI Parallelization 
Cross-platform interoperability
Machine Learning Support
Powerful Integrated Scripting Language
Latex File Output Model
Mixed Time Series Frequency report

Gretl Pricing: Gretl is distributed under GNU General public license and can be modified for personal use only.

Gretl Compatibility: Gretl could be installed and modified in Linux, MacOS and Windows.

Math Software for Engineers and Researchers

As an engineer or researcher, you need math software that helps solve complex and unstructured mathematics problems. Here are some of the powerful math problem-solving software for engineers and researchers.

SageMath is a free math software that combines the power of many existing open-source packages into a common Python-based interface. SageMath could also be used online and provides parallel computing capabilities making it an excellent choice for professional mathematicians and engineers.

SageMath Features:

Embedded graphics builder 
A wide range of built-in mathematical functions and libraries
Interfaces to more than 100 open-source packages
Advanced math like cryptography, group theory, commutative algebra, combinatorics, etc
Support for parallel computing with MPI
Multivariate and Univariate Polynomial

SageMath Pricing: SageMath is an open source and free math software program and can be downloaded from the SageMath website.

SageMath Compatibility: SageMath runs on Windows, macOS, Linux and could also be used on cloud.

Suggested Read: Free Online Courses to Enhance Your Skills for Career Success

GNUPlot is a mathematical graphing utility that produces high-quality 2D and 3D plots for complex mathematical equations. It offers a wide range of features for producing high-quality plots, including support for various types of data. It allows engineers and scientists to visualize data and mathematical functions interactively.

GNUPlot Features:

2D & 3D plotting
Interactive Data visualization
Direct file output ‘
Web display with mouse support
Non-interactive support including web scripting

GNUPlot Pricing: GNUPlot is a copyrighted but free-to-use graphing and math solving program.

GNUPlot Compatibility: GNUPlot runs on Windows, macOS, and Linux.

Maxima is a computer algebra system that enables engineers and scientists to solve complex mathematical problems. It offers a wide range of features for solving mathematical equations like manipulation of numeric and symbolic expressions. Maxima also offers a powerful scripting language that allows users to automate their workflows.

Maxima Features:

Symbolic integration 
ODE solver 
3D plotting 
 High precision numerical results

Maxima Pricing: Maxima is free open-source software released under the GNU General Public License.

Maxima Compatibility: Maxima runs on Windows, Linux, and Macintosh. Besides, its could also be installed on RPM and Debian based systems.

Suggested Read: Best Free and Paid eLearning Authoring Tools

In conclusion, there are many excellent math problem-solving software programs available for students, teachers, engineers, and researchers. Each program has its own unique features that make it well suited for specific types of mathematical problems.

Choose the program that best suits your needs and budget, and you’ll be on your way to solving even the most complex mathematical equations.

FAQs on Math Problem Solver Tool

Which software is best for mathematics?

Some popular choices among students, teachers and engineers for Math software include SageMath, GNUPlot, and Microsoft Math Solver.

What is the best free Math software?

Mathway, Microsoft Math Solver, and QuickMath are widely popular free math software among students and teachers.

What is the best Math software for PC?

Some popular choices for Math problem solvers for PC include Microsoft Math Solver, PhotoMath, and MathWay.

What is the best Math software for Mac?

Most of the open-source Math software are available for MacOS. GNUPlot, Maxima, and Gretl are some of the best math software for Mac.

Related Categories: Learning Management (LMS) Software | eLearning Software | Student Management Software | Student Information System | Knowledge Management Software

Rajan is pursuing CA with a keen interest in trends and technologies for taxation, payroll compliances, Tally Accounting, and financial nuances. He is an expert in FinTech solutions and loves writing about the vast scope of this field and how it can transform the way individuals and businesses... Read more

Sets - Problem Solving

Already have an account? Log in here.

This wiki is incomplete.

If $A = \{ 1,2,3,4 \}, B = \{ 4,5,6,7 \},$ determine the following sets: (i) $A \cap B$ (ii) $A \cup B$ (iii) $A \backslash B $ (i) By definition, $\cap$ tells us that we want to find the common elements between the two sets. In this case, it is 4 only. Thus $A \cap B = \{ 4 \} $. (ii) By definition, $\cup$ tells us that we want to combine all the elements between the two sets. In this case, it is $A\cup B = \{1,2,3,4,5,6,7 \} $. (iii) By definition, $ \backslash $ tells us that we want to look for elements in the former set in that doesn't appear in the latter set. So $A \backslash B = \{1,2,3\} $. $_\square$

Consider the same example above. If the element $4$ is removed from the set $B$, solve for (i), (ii), (iii) as well. (i) Since there is no common elements in sets $A$ and $B$, then $A \cap B = \phi $ or $A \cap B = \{ \} $. (ii) Because the element $4$ is no longer repeated, then $A \cup B $ remains the same. (iii) Since $A$ and $B$ no longer share any common element, $A\backslash B $ is simply equals to set $A$, which is $\{1,2,3,4 \} $. $_\square$

If $P=\{2, 5, 6, 3, 7\}$ and $Q=\{1, 2, 3, 8, 9, 10\},$ which of the following Venn diagrams represents the relationship between the two sets?

\[\large\color{darkred}{B=\{ \{ M,A,T,H,S \} \}}\]

Find the cardinal number of the set $\color{darkred}{B}$.

Note: The cardinal number of a set is equal to the number of elements contained in the set.

Bonus question given with the picture.

Join the brilliant classes and enjoy the excellence. also checkout foundation assignment #2 for jee..

Consider the set $ \lbrace{1, 2, 3, 4, 5, 6, 7, 8, 9, 10\rbrace}$.

For each of its subsets, let $ M $ be the greatest number. Find the last three digits of the sum of all the $ M $'s.

Assume that $0$ is the greatest number of the empty subset.

The number of subsets in set A is 192 more than the number of subsets in set B. How many elements are there in set A?

Problem Loading...

Note Loading...

Set Loading...

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

1.1: Introduction to Problem Solving

Last updated
Save as PDF
Page ID 9821

Michelle Manes
University of Hawaii

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

The Common Core State Standards for Mathematics ( http://www.corestandards.org/Math/Practice ) identify eight “Mathematical Practices” — the kinds of expertise that all teachers should try to foster in their students, but they go far beyond any particular piece of mathematics content. They describe what mathematics is really about, and why it is so valuable for students to master. The very first Mathematical Practice is:

Make sense of problems and persevere in solving them.

Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of the solution and plan a solution pathway rather than simply jumping into a solution attempt. They consider analogous problems, and try special cases and simpler forms of the original problem in order to gain insight into its solution. They monitor and evaluate their progress and change course if necessary.

This chapter will help you develop these very important mathematical skills, so that you will be better prepared to help your future students develop them. Let’s start with solving a problem!

Draw curves connecting A to A, B to B, and C to C. Your curves cannot cross or even touch each other,they cannot cross through any of the lettered boxes, and they cannot go outside the large box or even touch it’s sides.

$E1fb8f7ef76e399659c557f1a3f83d214.png$

Think / Pair / Share

After you have worked on the problem on your own for a while, talk through your ideas with a partner (even if you have not solved it).

What did you try?
What makes this problem difficult?
Can you change the problem slightly so that it would be easier to solve?

Problem Solving Strategy 1 (Wishful Thinking).

Do you wish something in the problem was different? Would it then be easier to solve the problem?

For example, what if ABC problem had a picture like this:

$e299328b7200743ea8fbd9fde138dacde.png$

Can you solve this case and use it to help you solve the original case? Think about moving the boxes around once the lines are already drawn.

Here is one possible solution.

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators  using SessionLab.

How do you identify problems?

How do you identify the right solution.

Tips for more effective problem-solving

Complete problem-solving methods

Problem-solving techniques to identify and analyze problems
Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve.

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward.

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

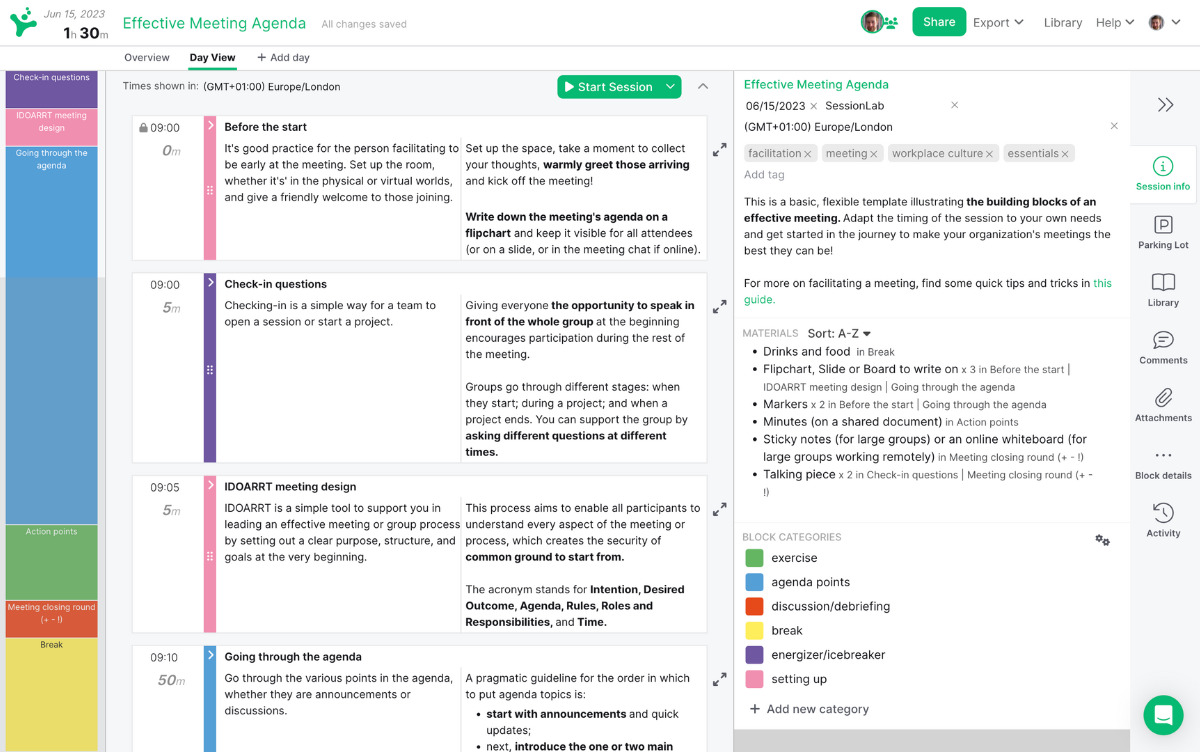
Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.

Try different approaches

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

Six Thinking Hats
Lightning Decision Jam
Problem Definition Process
Discovery & Action Dialogue

Design Sprint 2.0

Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on.

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages.

Lightning Decision Jam (LDJ) #action #decision making #problem solving #issue analysis #innovation #design #remote-friendly The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design.

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition #problem solving #idea generation #creativity #online #remote-friendly A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges.

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results.

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys #hyperisland #innovation This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold.

World Cafe #hyperisland #innovation #issue analysis World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD) #idea generation #liberating structures #action #issue analysis #remote-friendly DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology #action plan #idea generation #problem solving #issue analysis #large group #online #remote-friendly Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

The Creativity Dice
Fishbone Analysis
Problem Tree
SWOT Analysis
Agreement-Certainty Matrix
The Journalistic Six
LEGO Challenge
What, So What, Now What?
Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed.

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It! #gamestorming #problem solving #action Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed.

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable.

The Creativity Dice #creativity #problem solving #thiagi #issue analysis Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around.

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish.

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis #problem solving ##root cause analysis #decision making #online facilitation A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them.

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree #define intentions #create #design #issue analysis A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward.

SWOT analysis #gamestorming #problem solving #action #meeting facilitation The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results.

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause.

Agreement-Certainty Matrix #issue analysis #liberating structures #problem solving You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic . A problem is simple when it can be solved reliably with practices that are easy to duplicate. It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably. A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail. Chaotic is when the context is too turbulent to identify a path forward. A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.” The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process.

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID #gamestorming #project planning #issue analysis #problem solving When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!

Speed Boat #gamestorming #problem solving #action Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How #idea generation #issue analysis #problem solving #online #creative thinking #remote-friendly A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills.

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO!

LEGO Challenge #hyperisland #team A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems.

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken.

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What? #issue analysis #innovation #liberating structures You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists #vision #big picture #issue analysis #remote-friendly This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

Improved Solutions
Four-Step Sketch
15% Solutions
How-Now-Wow matrix
Impact Effort Matrix

21. Mindspin

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly.

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation.

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex.

MindSpin #teampedia #idea generation #problem solving #action A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result.

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution.

Improved Solutions #creativity #thiagi #problem solving #action #team You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged.

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch #design sprint #innovation #idea generation #remote-friendly The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper, Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change.

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change.

15% Solutions #action #liberating structures #remote-friendly You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference. 15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change. With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process.

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud.

How-Now-Wow Matrix #gamestorming #idea generation #remote-friendly When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice.

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them.

Impact and Effort Matrix #gamestorming #decision making #action #remote-friendly In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action?

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus.

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively.

Dotmocracy #action #decision making #group prioritization #hyperisland #remote-friendly Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

Check-in/Check-out
Doodling Together
Show and Tell
Constellations
Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute.

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out #team #opening #closing #hyperisland #remote-friendly Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start.

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems.

Doodling Together #collaboration #creativity #teamwork #fun #team #visual methods #energiser #icebreaker #remote-friendly Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team!

Show and Tell #gamestorming #action #opening #meeting facilitation Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible.

Constellations #trust #connection #opening #coaching #patterns #system Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic.

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree #thiagi #opening #perspectives #remote-friendly With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

One Breath Feedback
Who What When Matrix
Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space.

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round.

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them.

One breath feedback #closing #feedback #action This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward.

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved.

Who/What/When Matrix #gamestorming #action #project planning With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out!

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised.

Response Cards #debriefing #closing #structured sharing #questions and answers #thiagi #action It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks to build your agenda. When you make changes or update your agenda, your session timing adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore how to use SessionLab to design effective problem solving workshops or watch this five minute video to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you!

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.

Design your next workshop with SessionLab

Join the 150,000 facilitators using SessionLab

Using different digital tools in designing and solving mathematical modelling problems

Open access
Published: 18 March 2024

Cite this article

You have full access to this open access article

Melike Yiğit Koyunkaya ORCID: orcid.org/0000-0002-7872-3917 1 &
Ayşe Tekin Dede ORCID: orcid.org/0000-0002-8971-1970 1

773 Accesses

Explore all metrics

While existing studies acknowledge the importance of using technology in the mathematical modelling process, questions about how to integrate digital tools into mathematical modelling are not still answered. This study aims to examine pre-service mathematics teachers’ designing and solving mathematical modelling problems by using different digital tools through the collaboration of two different courses in their education program. The GeoGebra-supported modelling cycle was adopted as the conceptual framework of the study. The case study was used to design the research. The participants of the study were three volunteer pre-service secondary mathematics teachers, who were able to use and integrate digital tools in mathematics education. The pre-service teachers were asked to design a mathematical modelling problem by integrating different digital tools as the final assignment in both courses. The designed mathematical modelling problem, the video records of pre-service teachers’ explanations including the designing and solving process, and the video records of the focus group interview were the data of the study. The results showed that the pre-service teachers were able to design and solve an effective and comprehensive mathematical modelling problem using technology by combining their skills that they had learnt through different courses. In particular, they were able to use different digital tools in both designing and solving a mathematical modelling problem. Their solution also led to the extension of the adopted framework by adding new technological actions into the modelling stages.

GeoGebra as a Tool in Modelling Processes

Contradictions in mathematical modeling with digital technologies

Avoid common mistakes on your manuscript.

1 Introduction

Over the last decades, research has acknowledged the central role of using technology in mathematics education for contributing to students’ development of learning mathematical concepts, and digital tools Footnote 1 have been accepted as effective tools in learning and teaching mathematics (Bozkurt & Ruthven, 2017 ; Bozkurt & Yigit Koyunkaya, 2022 ; Clark-Wilson et al., 2014 , 2023 ; de Villiers, 1998 ; Laborde, 2001 ). In line with this idea, the use of digital tools to improve the teaching and learning of mathematical modelling has become an important research area (Greefrath et al., 2018 ; Kaiser et al., 2006 ). New technological tools (particularly digital tools) play a pivotal role in mathematical modelling by providing opportunities for exploring mathematical situations.These tools also foster new ways of understanding, evaluating, and interpreting real-world situations (Cevikbas et al., 2023 ; Molina-Toro et al., 2022 ). Although the use of technological tools in the mathematical modelling process has many advantages (Siller & Greefrath, 2010 ; Greefrath & Siller, 2017 , 2018 ), the question of how technology should be integrated into the implementation to effectively support students’ modelling skills has not yet been clearly answered (English, 2016 ). Although researchers have not yet been able to provide a clear answer to this question, ongoing research shows that more concrete studies on the use of technology in mathematical modelling are emerging.

Molina-Toro et al.’s ( 2019 ) research on the articulation of mathematical modelling and digital technologies and Cevikbas et al.’s ( 2023 ) research on the educational opportunities offered by digital technologies in mathematical modelling revealed that the importance of technology in modelling is of a current interest in the research area. However, a limited number of studies have been conducted on the effective integration of digital tools into learning environments (Siller et al., 2022 ). Hence, existing research (Cevikbas et al., 2023 ) suggested conducting studies on the opportunities and challenges of using different digital tools in mathematical modelling. Following this suggestion, in this study, we aim to extend this limited number of studies by concentrating on the use of different digital tools in both designing and solving mathematical modelling problems. In particular, we focused on how pre-service mathematics teachers (PMTs) used different digital tools to design a mathematical modelling problem and examined their solution throughout the modelling process by highlighting the intended use of different digital tools. Accordingly, the research questions are as follows:

How do PMTs use different digital tools in designing a mathematical modelling problem?

How do PMTs plan to solve a mathematical modelling problem using different digital tools?

The following section focuses on existing studies related to the aim of this study and discusses the selected conceptual framework that guided the study.

1.1 Importance of digital tools in mathematical modelling

The use of technology in mathematical modelling enables students to improve their modelling skills (Greefrath et al., 2018 ). The existing studies have illuminated the need for using technology to support the mathematical modelling process. For instance, Fuchs and Blum ( 2008 ) indicated that integrating technological tools into the modelling process could support students in achieving different goals. According to these researchers, the use of various digital tools at different stages of the modelling process could encourage students in terms of different pedagogical, psychological, cultural and pragmatical aims. These aims support students to learn application competencies in elementary or complex situations aimed at teaching; to comprehend and remember mathematical contents; to see a balanced picture of mathematics as a science and its impact on culture and society; and to understand, cope with, and evaluate known situations (Siller & Greefrath, 2010 ). From this perspective, students’ abilities to use digital tools could promote the approaches related to their solutions in the modelling process (Greefrath et al., 2018 ).

Existing studies have highlighted the advantages of using digital tools during the modelling process (Blum & Leiß, 2007 ; Greefrath, 2020 ; Greefrath & Siller, 2017 , 2018 ; Siller & Greefrath, 2010 ). In particular, using digital tools in this process supports the stages of the modelling process in terms of learning of mathematical concepts (Viseu & Leite, 2019 ), inquiring, reasoning and exploring some mathematical situations and concepts (Confrey & Maloney, 2007 ), realizing the importance of mathematical concepts in real life (Frassia & Serpe, 2017 ; Siller & Greefrath, 2010 ), constructing different representations (Arzarello et al., 2012 ), checking and validating mathematical solutions (Cevikbas et al., 2023 ), working experimentally (Villarreal et al., 2018 ), and making mathematical modelling a more accessible activity for students (Viseu & Leite, 2019 ). Furthermore, in the part of the modelling process, it is impossible to work on the problem without using digital tools in some cases. For example, it is inevitable to use digital tools in computationally intensive activities, in studying, structuring, or evaluating large data sets, in visualizing processes and results, and in some experimental studies (Siller & Greefrath, 2010 ) or in calculating and validating numerical and algebraic results (Greefrath et al., 2018 ; Lingefjärd, 2000 ). Therefore, teachers need to have comprehensive knowledge and skills in both using digital tools in mathematics education and integrating them into their teaching (Siller & Greefrath, 2010 ).

Lingefjärd ( 2007 ) states that if pre-service teachers are convinced of the benefit and necessity of using technology in mathematical modelling, they will be able to integrate it into their future teaching. From this viewpoint, it is important to educate pre-service teachers about the use of technology and mathematical modelling in their teacher education programs. Although researching the use of digital tools in mathematical modelling with pre-service teachers is crucially important to improve their teaching of mathematical modelling problems with the use of technology, Villarreal et al. ( 2018 ) assert that studies about the use of digital tools that support and enhance pre-service teachers’ knowledge and experiences in the modelling process are less prevalent. In one of these few studies, for example, Lingefjärd ( 2013 ) examined modelling tasks including technology and indicated that technology could broaden and enhance pre-service teachers’ experiences with modelling processes. In another study, Daher and Shahbari ( 2015 ) investigated middle school pre-service mathematics teachers’ modelling processes and concluded that the use of technology enabled meaningful mathematical learning. Therefore, we aimed to combine two different courses, Mathematical Modelling and Information and Communication Technologies in Mathematics Education, for educating pre-service teachers in terms of using digital tools to design and solve a mathematical modelling problem.

In the literature review on using digital technologies in modelling education, Cevikbas et al. ( 2023 ) stated that although there were well-founded findings about modelling with digital tools, many concrete questions remain unanswered. One of these questions is how technology is used for modelling and what the interaction between humans and media is (Schukajlow et al., 2018 ). In our study, we illuminated how technology was used for modelling by investigating which and how digital tools were used in both designing and solving a modelling problem. This study, in particular, extended the existing literature about the use of digital tools in designing and solving a mathematical modelling problem by suggesting the use of different digital tools such as GeoGebra, Desmos (particularly a graphic calculator), Google Earth, or Youtube, which have not been used together in both designing and solving a mathematical modelling problem with technology before. In the next section, we present Greefrath et al.’s ( 2018 ) framework that leads the examination of the modelling problem solution process.

1.2 Conceptual framework

The use of technology plays a pivotal role in the modelling process, which cannot be accepted as an independent domain. Therefore, digital tools can be usefully integrated in every stage of the modelling cycle (Geiger, 2011 ; Greefrath et al., 2011 ; Greefrath & Vorhölter, 2016 ) depending on the purpose (Ludwig & Jablonski, 2021 ). Although different digital tools used in the modelling cycle have been discussed in the studies, the researchers mainly used dynamic geometry software (specifically, GeoGebra) or computer algebra software. In particular, these studies indicated that GeoGebra supports the modelling process through the use of program-specific features such as using different kinds of representations, self-checking by comparing chart and spreadsheet windows or controlling the geometric constructions by changing a point (Greefrath & Siller, 2018 ). In this study, Greefrath et al.’s ( 2018 ) GeoGebra-supported modelling cycle, which describes technological actions on Blum and Leiß’s ( 2007 ) modelling cycle, was chosen as the conceptual framework to examine the pre-service teachers’ possible solution in the modelling process (see Fig. 1 ).

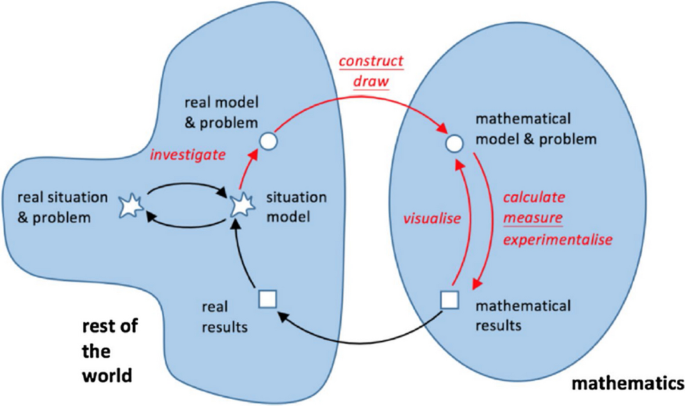
GeoGebra-supported modelling cycle (Greefrath et al., 2018 , p. 236)

According to Blum and Leiß’s ( 2007 ) cycle, first students understand a real-life problem and construct a situation model explaining the problem. Then, they simplify the situation model and construct the real model by making the necessary assumptions. During the mathematization process, students construct mathematical models and then obtain mathematical results by solving the models. Students consider mathematical results in the context of real life situation, discuss the effectiveness of the results, and obtain real results by interpreting them. They validate real results by re-examining assumptions, mathematical models, mathematical results, and correctness of calculations (Tekin Dede & Bukova Güzel, 2018 ). The technological actions that occur when the use of digital tools is integrated into the modelling process are shown in red ink in Fig. 1 . Greefrath et al. ( 2018 ) developed the cycle based on empirical data and found that GeoGebra was only applied in the modelling cycle among the construction of a real model, a mathematical model, and mathematical results. Particularly, in this figure, the actions of investigate, experimentalise, calculate and visualize are the actions that could be confirmed by empirical data, but the researchers added other actions (construct, draw and measure) by working on GeoGebra (Greefrath et al., 2018 ). In the aforementioned study, they did not find any evidence for the use of GeoGebra in other steps of the modelling cycle due to reasons such as the small number of students or the problem itself. However, in their previous studies, they stated that visualization and controlling/verifying are possible technological actions that can be used in the transition from mathematical results to real results, in other words, in the interpretation step as several possibilities for applying digital tools in the modelling cycle (Greefrath, 2011 ). These technological actions are adopted and interpreted as given in Table 1 .

For the examination of the actions, there are studies in which GeoGebra is used as a digital tool. In contrast to the existing studies, in this study, we suggest a new perspective on technological actions on the modelling cycle by providing different digital tools that can be used in both designing and solving mathematical modelling problems. In addition, we aimed to expand the use of digital tools in the stages of modelling cycles, such as the validation stage, where student work is rarely seen (Blum & Leiß, 2007 ), in response to Greefrath and Vorhölter’s ( 2016 ) call regarding the necessity of extending the modelling cycle and the necessary translation process (e.g. interpreting and validating) by using digital tools.

In this study, a qualitative research paradigm was adopted and the research was designed using a case study. The case study examines and answers the research questions of what, how, and why to analyze the identified case in depth in its context or environment (Yin, 2018 ). Using the case study design helped us explore the PMTs' ability to design and solve a mathematical modeling problem with the use of different technological tools, which also showed us the effects of integration of two courses in a teacher education program. In particular, we accepted the PMTs’ designing and solving of a mathematical modelling problem as a unit to understand and illustrate the process, in detail (Stake, 2005 ).

2.1 Participants, context, and procedure

The participants of the study were three pre-service secondary mathematics teachers in their third year of the teacher education program in Türkiye. We conducted this research by combining two different university-based courses during the Spring Semester of 2021. Two authors were instructors of different courses namely Mathematical Modelling (MM) and Information and Communication Technologies in Mathematics Education (ICTME). The MM course (21 PMTs were enrolled in this course) was compulsory, and the ICTME course (14 PMTs were enrolled in this course) was the elective course in their program. Fourteen PMTs were taking both courses, and we selected three of them based on a purposive sampling method (Merriam, 1998 ). In particular, we considered a couple of criteria in selecting the participants of the study. The PMTs’ use of different technological tools in designing and solving mathematical modelling problem is our first criterion. Most of the students integrated technology into their mathematical modelling problems, but the selected participants used various technological tools for different purposes while designing and solving their problem as the final assignment. Additionally, their ability to use of technological tools was considered another criterion in the selection. These three PMTs provided evidence regarding the development of their ability to select, appropriately use, and integrate technological tools in designing technology-based tasks during the course. Based on the authors’ experiences in the courses, the PMTs’ ability to explain and justify their thoughts, reasoning, and decisions was considered as another criterion, which was a crucial aspect in both collecting and examining the data. In addition, these three participants had different academic achievements, and they were willing to participate in the research and volunteered for participation. The PMTs also indicated that it is almost impossible to solve their modelling problem without using technology, which also supported our decision to work with these pre-service teachers.

Even though two different courses have different aims and outcomes, as instructors, we discussed and collaboratively worked to combine some parts of the courses. The MM course aims to teach PMTs how to learn and realize the nature of mathematical modelling and modelling process; to be able to design and solve mathematical modelling problems; to learn how to use technology in mathematical modelling; and to understand the place of mathematical modelling in the curriculum. The ICTME course aims to provide students with the ability to integrate different technological tools into mathematics education and to use dynamic mathematics software (particularly GeoGebra), various web 2.0 tools (particularly Desmos), and web-based education applications. The goal of this course is not only to improve students’ ability to use technology in mathematics education but also to develop their existing mathematical knowledge by discussing the role of technology in mathematics teaching and learning. The contents of the courses are given in Table 2 . As instructors, we discussed and selected a few mathematical modelling problems that were designed or solved in technological environments. In the same week, while implementing the example, the instructor of the MM course introduced and discussed how to solve modelling problems throughout the stages of the modelling cycle by using technology. The instructor of the ICTME course taught and discussed how to design or solve problems using various technologies and how to use the interface or technological tools in these technologies. For instance, in week 11, we provided the Buca Arena Stadium problem (Yiğit Koyunkaya & Tekin Dede, 2021 ) to the PMTs, and the instructor of the MM course taught how to design the problem considering the stages of the modelling cycle. The instructor of the ICTME course taught how to create and construct a custom activity in Desmos by focusing on how to integrate pictures or videos, how to add the notes, free-response, math-response, multiple choice, checkbox or order list, media and links, how to use the graphic calculator, sketching or geometry tool, and discussing the importance of adding the teachers’ role, students’ support, and sample responses. At the end of the courses, 14 PMTs were required to do a final assignment in which they had to design a mathematical modelling problem in Desmos. In the assignment, the PMTs were also asked to use/integrate various technologies learned in the ICTME course, and they were free to work in groups (including 2 or 3 people). In the assignment, the PMTs were asked to design the problem in Desmos by considering mathematical modelling problem criteria (Borromeo Ferri, 2018 ) and a possible solution regarding the stages of modeling cycle (Blum & Leiß, 2007 ). In each Desmos window, they were free to select and integrate any digital tools and were required to include teachers’ role, students’ support, and sample responses. Additionally, they were required to prepare a report explaining the design and solving process. They were free to select the type of their reports; some of the PMTs prepared a written report while other returned audio/video records.

The data in this paper were collected through one group’s final assignment of the courses. The three selected PMTs were members of one group, and they designed a modelling problem in Desmos by integrating various technologies into it and solved it in GeoGebra and Desmos.

2.2 Data collection and analysis

The data of the study consisted of a modelling problem ( Festival in the City ) Footnote 2 designed by the three PMTs as a group in Desmos, files related to a possible solution in both Desmos and GeoGebra, three video records in which the PMTs explained their design and solving of the problem that captured their screen and voice, and a video record of the focus-group interview. As a final assignment, the PMTs initially designed mathematical modelling problem using the criteria and constructed 14 windows in Desmos by considering the stages of the modelling cycle. In the assignment, they were required to prepare a report, and the selected group preferred to return their report as video recordings. In the report, they self-recorded three different videos to explain their reasoning of their actions regarding the design process, content, and possible solution of the problem using digital tools. In all of the video recordings, the PMTs used a program to record both the computer screen (in which they introduced or solved their mathematical modeling problem) and their voice. In the first video, they explained how they used a particular tool in each window in Desmos, and how and why they used and integrated different digital tools in different windows (The length of the video was 6 min.). For instance, while explaining the second window in Desmos, they explained how and why they provided YouTube and Google Earth links. In the second video, for each Desmos window, they focused on explaining how a teacher could implement the task by indicating the teachers’ role, students’ support, and sample responses regarding the problem (The length of the video was 10 min.). In the last video, they explained how the problem could be solved using both GeoGebra and Desmos, and solved the problem using GeoGebra first and Desmos then (The length of the video was 15 min.). In that video, they also discussed the challenges they faced while solving the problem as well as affordance related to solving the problem with the use of digital tools. After initially examining their problem and video-based reports, we prepared semi-structured questions to reveal their thoughts, decisions and reasoning about the whole process in the focus group interview. In the interview, two researchers and three PMTs met, and the video camera zoomed in on the PMTs’ computer screen and captured their voices. Throughout the focus group interview, they discussed the content of each Desmos windows to reveal the PMTs’ aims in using digital tools throughout the mathematical modelling process. For instance, we asked them “What are your expectations from students in window 7? Why did you prefer to add the graphic calculator in this window? What is the role of this window in the modelling process?”, “What are your goals in adding the teachers’ role and students’ support in each window?”, and “Why did you use both GeoGebra and Desmos for the possible solution of the problem?”, etc. The focus group interview was conducted over 60 min.

In the analysis, we initially examined the modelling problem in each window in Desmos by examining which digital tools the PMTs used and how they used these tools in each stage of the modelling cycle. After identifying the digital tool, we focused on how the tools served the modelling process by considering the codes identified by Greefrath et al.’s ( 2018 ) study. We then transcribed all the records of their video-based reports and focus group interview. After transcribing, we initially read whole data and divided it into parts in terms of the stages of the modelling cycle considering Blum and Leiß’s ( 2007 ) study. In each part, we identified and colored the digital tools and examined how the digital tools were used to support the related stage. To reveal their purpose of using the digital tools, we coded the technological actions in terms of Greefrath et al.’s ( 2018 ) framework. In this process, in addition to the identified codes, we also found new codes regarding PMTs’ use of digital tools in the stages of the modelling cycle, and extended the existing framework by adding new technological actions.

In the analysis, we used a six-row table, and an example of the table can be seen in Table 3 . In the first row, we took a screenshot of the examined Desmos window, and labeled which digital tool the PMTs used in the second row. The table also included a third row that explained how the PMTs used the digital tools (particularly in this step, we looked for the function of the tool in the problem). The fourth row represented the PMTs’ planning that focused on what they suggested to the teachers and how they planned to support the students while implementing the problem. In the fifth row, we analysed how digital tools serve the modelling process by considering the stages of the modelling cycle and the technological actions within the framework (Greefrath et al., 2018 ). The last row included the PMTs’ quotes from the video records or from the focus group interview that explained the design process of the problem, and suggestions for teachers during the implementation. We used these quotes to support our analysis of the use of digital tools in the design process of the problem.

Afterwards, we analyzed the transcriptions regarding the problem’s possible solution in both GeoGebra and Desmos by using the components of the framework (Greefrath et al., 2018 ). For this purpose, we initially re-read the the entire transcription, re-examined the PMTs’ solution approaches in GeoGebra and Desmos, and identified the PMTs’ modelling approach in each stage of the cycle (Blum & Leiß, 2007 ). Additionally, we examined how the selected digital tools served their solution in terms of their modelling approach. In this process, we also identified the technological action they performed to reach their intention. For instance, if the PMTs constructed mathematical models in their possible solution, we coded their work as their approaches in the mathematization stage. Related to their solution, in the focus group interview, the PMTs explained how and why they found the area under the curve by using the graphic calculator, and we related that part to the mathematization stage in the analysis.

In this process, we used another table, as shown in Table 4 . The first row represents the screenshot that showed which digital tool (GeoGebra or Desmos) the PMTs used and their purpose of using it; the second row includes the modelling stages; the third row explains how they used the digital tools for solving the problem (particularly we focused on the function of the tool in the process); the fourth row represents the technological actions they performed to solve the problem; and the last row includes the PMTs’ quotes from the video records.

To increase the validity of the data, we triangulated different data sources by focusing on the roles and functions of digital tools in designing and solution of the mathematical modelling problem, which also helped us ensure the trustworthiness of the data. To ensure the reliability, we analyzed the whole data together and discussed our different codes and interpretations until we reached a consensus (Miles & Huberman, 1994 ). After 3-months, we re-analyzed the whole data to ensure the stability of the analysis (Krippendorff, 1980 ). Additionally, we provided a consent letter to the PMTs by indicating that their names were anonymous, their participation was voluntary, and they could withdraw from the study at any time without providing any reason (Patton, 2014 ).

In this section, we present the design process of the PMTs’ modelling problem and their possible solution approaches using different digital tools. In the text, the bold words represent the technological action identified through the process and the italics represent the digital tools used by the PMTs. We have added these actions to Greefrath et al.’s ( 2018 ) framework and expanded it as presented at the end of this section.

3.1 Design process of the problem

The PMTs planned to implement the warm-up step of the problem by integrating images or videos in four different Desmos windows. In the first window, they used images of the bridge taken from different perspectives/angles and planned to use them as a visual amplifier. They, particularly, aimed to contribute to realism by providing different pictures of the bridge for students without real life experience regarding the context. PMTs explained their actions as follows:

In fact, we intentionally used the pictures. At the beginning, we only included one picture of the bridge; however, we wanted students not to look at the bridge from a single viewpoint. We aimed to support the students in discovering the bridge by looking at it from different perspectives. We thought that students may find different approaches regarding the solution to the problem, or they may start to solve the problem using different solution strategies. Therefore, we have added different pictures of the bridge.

Additionally, in these windows, the PMTs included various supportive actions for teachers that could be used while implementing the problem (see Fig. 2 ). For instance, they suggested implementing the problem in a 2-hour lesson, dividing the students into groups (4–5 people in each group), and giving 3 min. for students to examine the problem.

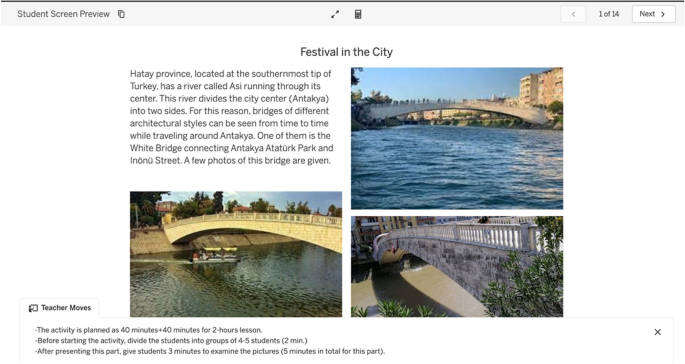
Different images of the bridge

In the second window, the PMTs used a video-based application as a technological tool, and they thought of doing warm-up exercises for the real appearance of the bridge with a 30-second video recorded over the bridge (Youtube) Footnote 3 and a web-based application (Google earth) Footnote 4 . Regarding the reasons for using these digital tools, they stated that some students may take objects of different scales on the bridge as a reference to construct the model, and it would be useful to allow them to explore these objects better to calculate the possible length and area related to the bridge. They expressed their purpose as follows:

We thought that students could think as if they were on or near a bridge using these tools. We also considered that the pictures may not be sufficient to provide an approach to solving the problem. The objects are a little far away in the pictures, but by using Google Earth, they can visualize the people and use them as a reference. In addition, you can walk around the bridge using this tool. We have added it to visualize the real context … We could not have described the bridge in any other way without the use of these digital tools.

The PMTs considered that the technological tools integrated into the problem provided students with the opportunity to experience and explore the real situation related to the existing condition of the context. As a warm-up activity, to support the students’ exploration and experimentation with the context, the PMTs also added two windows that included questions about the advantages of the bridge to the city, and whether they have ever seen a similar bridge. In the interview, they explained the purpose of adding the warm-up activities as supporting the students in visualizing the context of the bridge in their minds and enabling different solution strategies regarding the use of different objects around or on it (See Fig. 3 ). In this sense, the tools used by the PMTs in the warm-up step of the modelling cycle contributed to the exploration , visualization, and experimentalization of the context.

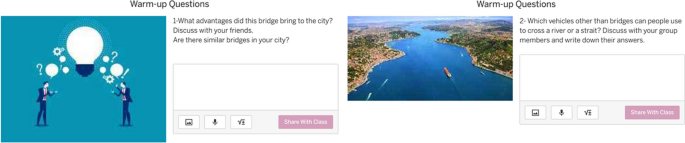
Warm-up activities in the two windows

In the fifth window, the PMTs presented the modelling problem, and they expected students to read and understand the problem (See Fig. 4 ). The PMTs emphasized that it is crucially important for students to understand the problem, so they planned to use the ‘Students Support’ tab in the Desmos. In this sense, as student support, they provided the following suggestion; ‘If any group has difficulties in understanding the problem, you (as a teacher) lead them and give a clue about where they should start to solve the problem.' They also planned to help with questions such as ‘What do I need to know first to determine how much paint to use?’ or ‘What do you think about finding the length of the cable? How can we find the length?’. The PMTs thought that these questions could trigger students’ thinking about finding knowledge regarding the real-life context. In other words, these questions encouraged students to construct a situation model and transition to a real model by simplifying the problem.

The modelling problem

The next windows comprised sections designed to calculate the total area of the surfaces to be painted and the lengths of the LED cables to be installed on the bridge. These steps (the following eight windows in Desmos) included, respectively, windows for making predictions (6 and 10), graphing calculator windows for constructing mathematical models (7 and 11), windows for solving the mathematical models using real life data (8 and 12), and windows for comparing the results obtained by solving the mathematical models with the predictions (9 and 13). In detail, in the sixth window, the PMTs planned to encourage students to make a prediction about the solution of the problem, and they considered measuring and assessing students’ modelling approaches through comparison (See Fig. 5 ). This prediction activity could support students’ transition from the situation model to the real model. The PMTs expressed the reason for adding prediction windows as follows:

We asked about their predictions because we wanted the students to compare whether they could get closer to the value they predicted when they reached the result. We wanted them to realize how close they had come to the exact result and to see the difference between them.

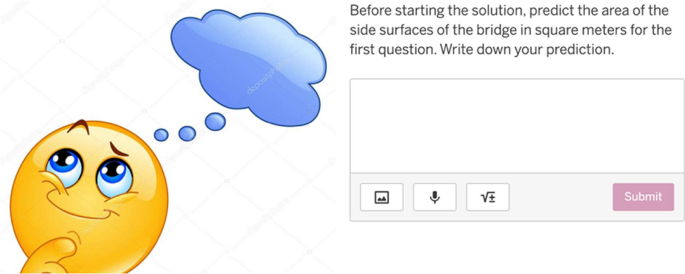
Prediction activity

In the following window, the PMTs planned for students to construct a mathematical model for finding the area of the bridge to be painted. In this window, using the graphical calculator in the Desmos, the PMTs planned for students to construct parabolas representing the bridge and calculate the area between the parabolas with the help of the integral to determine the surface area of the bridge.

In window 8, by providing a free response feature in Desmos, the PMTs planned to ask students to search the properties of the paint they planned to use for coloring the bridge (as well as the LED cable in the following windows), and explain why they chose that particular paint. At this stage, the PMTs aimed for students to identify the assumptions they should use to solve the mathematical models by comprehensively using search engines . They explained their intention as follows:

Searching on the internet is of crucial importance in calculating the cost of paints. We expect them to calculate the cost in the most appropriate way by including these studies in their work.

In the following window, the PMTs aimed for students to compare their predictions with their mathematical results. In particular, this window is effective in validating the solution to the problem. Similar to the previous windows, the PMTs designed the next four windows (10–13) by following similar steps to find the length of the arc using the concept of integral. Similarly, their main expectations from students are to find the length of the LED lights required for the decoration of the bridge and to validate their predictions for the cost calculation by comparing it with their results. In these stages, the PMTs planned to use the graphic calculator in Desmos and search engine tools.

In the last window of the problem, the PMTs planned for students to perform self-validation through the stages of the modelling cycle in the checklist. This checklist is helpful to validate students’ approaches regarding the stages of the modelling cycle, including understanding the problem, simplifying, and evaluating the mathematical model and its’ solution. Additionally, they used a free-response feature to reveal students’ thoughts regarding the advantages and disadvantages of solving the problem using digital tools.

3.2 A possible solution to the problem

The PMTs used both the GeoGebra software and the graphic calculator in Desmos to solve the designed problem. Initially, they considered that the mathematical concept to represent the bridge could be a curve or a function. In line with this idea, they first focused on investigating and visualizing the real-life context given in the problem to construct a situation and real model of the problem. They chose a picture given in the warm-up activities in the first window while constructing the real model. They explained their reasoning for choosing the picture as follows:

They [Students] need to identify the most useful picture so that they can easily calculate the area and the length of the curve… The student should be able to identify and select the necessary picture for the solution. The selected picture should be taken from a wide angle to determine and calculate the length and scale.

According to the PMTs, they selected the most appropriate picture to work on their necessary predictions while constructing the model. Then, they decided to construct the mathematical model in GeoGebra and initially added the picture to the screen using the insert image tool. While inserting it, they intentionally positioned the left corner of the picture at the origin and parallel to the axes.

After the PMTs placed the image on the coordinate plane, they began to work on the mathematization stage. They considered the possibility of using the parabola to calculate the surface area and the lengths of the arcs, and continued to work on the mathematical model. In line with this purpose, they initially decided to determine the boundaries of the bridge by drawing the parabola on GeoGebra. During the drawing process, they thought that experimenting with the software could help contruct the mathematical model. While experimenting, they considered that the bridge could be a curve; therefore, they needed to find a quadratic equation to represent it. At this stage, the PMTs attempted to construct the mathematical model and to find the necessary equation by performing different experiments on the software. For instance, they considered using circles (particularly an arc on the circle) to construct mathematical models and used the circle tool in GeoGebra to find the length of the LED lights (See Fig. 6 ). Additionally, they focused on the sector on the circle to calculate the surface area and the lengths of the arcs. They drew circles as shown in Fig. 6 ; however, by working on the circle, they were not able to construct the mathematical models.

PMTs’ intention to solve the problem

They explained their actions as follows:

At one point, we even stated that a curve could be found using a sector instead of a parabola. Then, we drew a circle that could be placed on the bridge. At first, we thought that the circle matched better with the bridge; however, the circle was too big [they indicated that the center was far away from the bridge for calculations on the screen as given in Fig. 6 ].

The PMTs then decided to work on the parabola to construct the mathematical model. In this process, they decided to work on the equations $\text{a}(\text{x}-\text{r})^2\text{and} \ \text{b}(\text{x}-\text{r})^2$ , and constructed two sliders to represent the coefficients a and b using the slider tool in GeoGebra. They intentionally drew two different parabolas because one of them represented the upper side of the bridge, and the other represented the lower part of the bridge. In the screen, the PMTs constructed slider a (representing the coefficient a for the parabola in the red color) to draw the parabola for bounding from the bottom and slider b (representing the coefficient b for the parabola in the blue color) to draw the parabola for bounding from the top (See Fig. 7 ).

PMTs’ drawing of parabolas in GeoGebra

The PMTs' explanation regarding the process of constructing the quadratic equations is as follows:

We started by writing a random parabola equation and then changed the coefficient a. However, we could not find the exact parabola representing the bridge. While thinking about how we can do it, we finally thought to find the vertex, and then we can work on it. Next, we drew two different parabolas with coefficients a and b, and the vertex was exactly centered on the bridge. We dragged the sliders to precisely position the arms of the parabola over the bridge.

By experimentalizing the image, the PMTs initially attempted to find the parabola equation representing the curves on the bridge. When they realized that it was impossible to find the value of coefficient a using this, they decided to drag the slider to represent the coefficient. At this point, they wrote a general formula for the quadratic equation on the input tool in GeoGebra and used the slider’s increment feature to determine the exact values of coefficients a and b (which were negligibledecimals). Then, by dragging the slider , they found the coefficients required for the best positioning parabola equation formed the curve of the bridge. In this process, the PMTs attempted to construct the mathematical models by experimenting with the slider tool . In their own words, they explained their actions as follows:

We used the zoom in tool to enlarge the image… We changed the settings of the slider to place the curve exactly on the bridge. We assigned value as 0.001 in the slider and struggled to find the exact value of the coefficient a. As difficult as it was, it was a fun process for us anyway; we think that it was much simpler than the normal solution process… After finding the first parabola equation, everything was easier, and we found the other parabola using the same method.

The PMTs’ actions related to finding the exact value of the coefficients revealed that they validated and verified their initial mathematical models, and revised these models (See Fig. 8 ).

PMTs’ drawing of the parabolas on the bridge

Afterwards, in the working mathematically stage, the PMTs reached the mathematical results (shared in the following paragraphs) by solving the models they constructed. In this process, to find the results, they used the integral command in GeoGebra.

After experimenting in GeoGebra and constructing the necessary mathematical models, the PMTs also solved the problem using the graphing calculator in Desmos (windows 7 and 11 in the problem). After inserting the selected image into Desmos, the PMTs initially determined the boundaries of the quadratic equation representing the parabola. Hence, they set the boundaries as the interval [-9,9], as shown in Fig. 9 , and arranged the position of the image such that the starting and ending points of the bridge coincided on the x=-9 and x = 9 lines (see Fig. 9 ). At this stage, the PMTs constructed the real model needed to solve the problem by simplifying.

PMTs’ solution approach in Desmos

After determining the boundaries, similar to their actions in GeoGebra, they constructed the algebraic expressions of the parabola (in other words, mathematical models) representing the upper and lower boundaries of the bridge (See Fig. 10 ). The PMTs stated that they determined the coefficients of the equation by experimenting and indicated the differences between GeoGebra and Desmos in this process as follows:

By experimentation, we changed the coefficients and the position of the vertex and tried to fit the parabola on the bridge. In this section, the GeoGebra software has a little more advantage than Desmos. However, Desmos also has other advantages; for example, calculating and writing the integral formula better, easier, and fast.

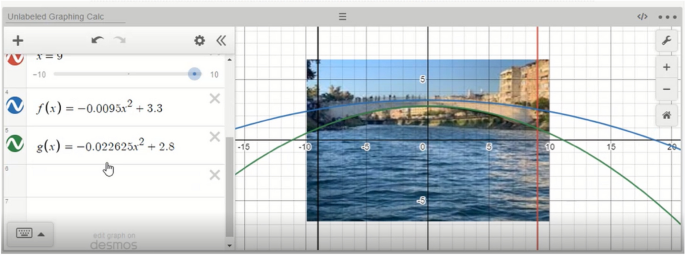
PMTs’ drawing of the parabolas using the graphic calculator

After constructing the mathematical models for the identified intervals and drawing quadratic equations, the PMTs solved the models using definite integrals. In the working mathematically stage, the PMTs calculated the arc length and the area under the curve using integral formulas similar to the actions performed in GeoGebra. They worked on the graphic calculator and calculated the area between the two curves and the lengths of the arcs (see Fig. 11 ).

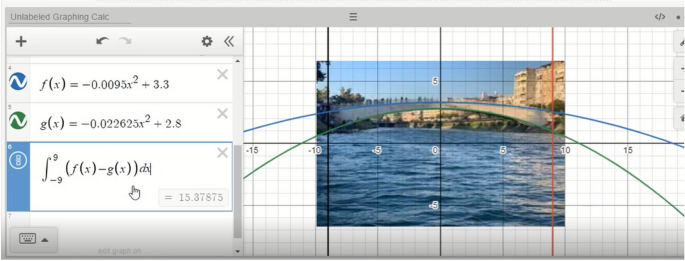
PMTs’ integral calculation in the graphic calculator

However, as seen in Fig. 11 , their solution was not correct because the mathematical model they constructed for the arc length was incorrect (they forgot to take the derivative of the function) (see Fig. 12 ). Then, they realized that they had misremembered the formula for the length of the arc with a definite integral, and afterwards, they revised their solution (as we mentioned in the following paragraphs).

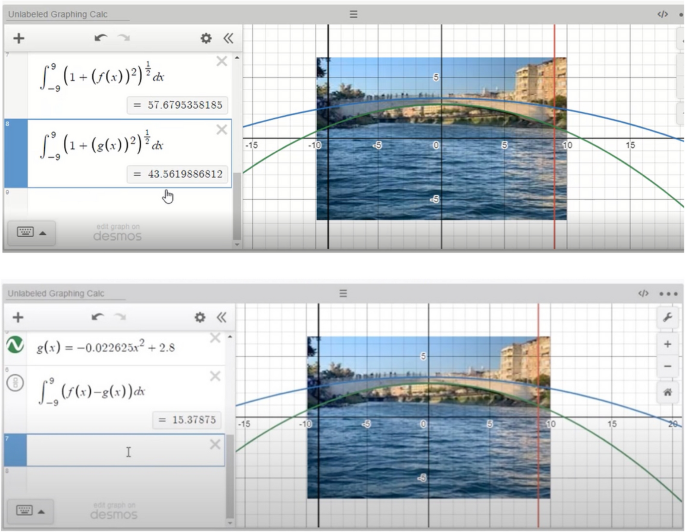
PMTs’ incorrect solutions

By solving the mathematical models, the PMTs found the arc lengths to be approximately 57.7 and 43.6 units, respectively, and the area between the curves to be approximately 15.4 square units. The PMTs then needed to transform the numerical solutions they found in units into real-life conditions. The PMTs considered the different objects in the image and decided to use the height of a person on the bridge as a reference point. To identify the real value corresponding 1 unit, they first decided to find how many units equal the average person height using the graphic calculator in Desmos. At this point, the teachers drew a line segment corresponding to the height of a person, and measured and calculated the length of this line segment as 0.59 units. They made a prediction regarding the average height of a person as 1.65 m, and focused on solving the problem using their assumption. By proportioning, they assumed that 1 unit corresponds 2.79 m with the help of a calculator . In this process, by calculating , the PMTs transitioned from the mathematical results to the real results. They explained this process as follows:

At this point, I should take these values and apply them to real life. For this, I need to determine the unit. To determine the unit, we used the height of the person over there. When I zoomed [zooming in and showing a person on a bridge], we determined two points from the head to the foot of this person. This made 0.59 units. As a result of research on the internet, we found that the average height of men in the world is 1.70 and that of women is 1.60. We took the average because we did not know the gender of the person. We took the person’s height as 1.65 m. Thus, 0.59 units correspond to 1.65 m. This means that 1 unit is 2.79 m. Then, if we use the unit, we found for the integral value we found here, the students will reach the real value because of the calculation.

They calculated the area between the curves to be approximately 120 m 2 as a real result. They found the total area to be approximately 240 m 2 considering the two sides of the bridge. They previously found 207 m 2 in GeoGebra, and by comparing the two results, they evaluated both results and stated that they found close values even when using different digital tools. During the verification process, they expressed their thoughts regarding the differences between Desmos and GeoGebra as follows:

In our previous solution in GeoGebra, we found approximately 250 m 2 . Therefore, we can actually say that we found almost the same values. Because after all, the people we take as a reference are different. Here (Desmos), the picture is a little blurred in Desmos. It is a bit clearer in GeoGebra. In Desmos, this clarity is a bit more distorted. It also has an effect on determining the points. This difference may be because of that. However, when students find values almost similar to this, it is acceptable.

Subsequently, they calculated the lengths of the arcs using the same unit measure and realized that the mathematical model they constructed was not correct. Hence, they needed to revise the integral formula and the mathematical models in the graphic calculator, as shown in Fig. 13 .

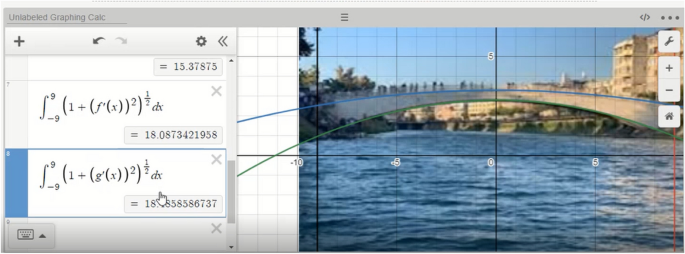
PMTs’ revised formula for the integral

After their revision, they re-calculated the necessary values using a calculator . They found the length of the upper curve to be approximately 50 m. and the length of the lower curve to be approximately 51.5 m. The PMTs stated that the values they found in GeoGebra were 44.5 and 46 m, respectively, and emphasized that they verified the solution considering the close values they found. Their revisions illuminated that PMTs validated their mathematical models and solutions.

After solving the mathematical models, they searched the engine based on the real-life data necessary to find the costs. As a result of their searching, they assumed that 1 L of paint could be used to paint 7 m 2 area, and the total cost would be approximately 3800 TL. In addition, they calculated the cost of 10 m led light as 87,20 TL. The PMTs interpreted the real results in terms of the real context by considering an economic solution as follows:

After this, students will search for the necessary values. Because of this research, they will identify which paint is more suitable and economic, which led light is better, and then calculate the cost. The students’ answers could be different at this point.

The PMTs revealed two different solution approaches by solving the designed modelling problem in both GeoGebra and Desmos. They stated that they initially solved the problem in GeoGebra and transformed their solution to Desmos because they validated their solution in Desmos. Regarding the digital tools they used to solve the problem, they indicated the following:

We really don’t know how we could solve the problem without using GeoGebra or Desmos. We really tried to solve it and thought about the solution, but it is impossible to solve it on paper. I mean, we could draw the curves with a paper and pencil if we had the skills of an architect, but that is not possible for us. In this way, it is crucially important to teach students that such tools are really effective for solving these types of problems. They can solve the problems with 4–5 actions in these digital tools.

The PMTs’ approaches for solving the problems revealed that various digital tools and their features could be used differently and effectively in solving a mathematical modelling problem. The technological actions of the PMTs’ used in the solution process led to the development of the adopted conceptual framework of the study (see Fig. 14 ). In particular, their possible solution of the problem using different digital tools (dynamic mathematics software, web 2.0 tools, video-based application, web-based application, calculator, search engine) led us to extend the framework by adding a couple of technological actions. In detail, while constructing the situation and the real model, they planned to implement the warm-up activities using visual amplifiers or video/web-based applications. Their actions demonstrated their intention to support students by encouraging them to visualize and imagine (or have an experience if they did not know the context) the real-life context. In particular, the visualization action was effective in selecting and using the most appropriate image/picture when constructing the situation and real model required to solve the problem. In this sense, visualization could be defined as “providing visual amplifiers or video/web-based applications to construct the situation and real model”. Afterwards, while constructing the mathematical models, in addition to constructing and drawing, the PMTs tried to find the quadratic equation by experimenting with GeoGebra software (i.e. using the circle). While experimenting with the parabola equation to construct the most appropriate mathematical model for solving the problem, they benefitted from the dynamic features of the digital tools by adding and dragging the sliders. In particular, dragging provided a crucial effect when experimenting was not sufficient for mathematical model construction that best fits the real model. In this context, we defined the experimenting as “assumptions and conditions tested using the dynamic features (i.e. dragging) in the digital tools”. Dragging action could be defined as “providing immediate feedback to realize the instant changes in the mathematical model based on the assumptions and conditions”. Additionally, the action of calculation could be described as “calculating numerical or algebraic results by conducting operations on any digital tools”. Then, they verified their mathematical model by experimenting with different quadratic equations at the end of the mathematization step. We defined verification as “a judgment based on acceptance, revision, or rejection of the mathematical model”. While transitioning from mathematical results to real results, they used the real data by operating on the calculator to construct the representation of the real data and then calculated the necessary values. They solved the problem using two different digital tools and compared their results to support them verify the real results. In this step, the definition of verification could be similar to the given one, and accepted as “a judgment appeared based on acceptance, revision, or rejection of the real results”. We accepted the definitions of other actions that occurred in the solution process similar to those given by Greefrath et al. ( 2018 ). The figure given below (Fig. 14 ) represents the revised cycle, and the actions given in orange text were added by the authors.

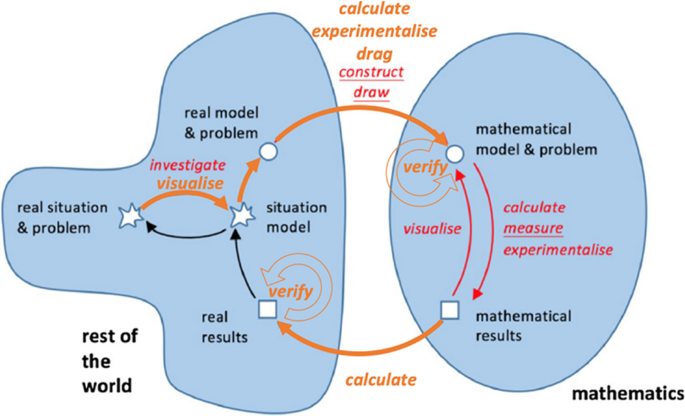
Digital tool-supported cycle

4 Conclusion and discussion

The main goal of this study is to examine the PMTs’ designing and solving mathematical modelling problem using different technologies. In this regard, the PMTs designed their problem in Desmos using various pictures, videos, and links (i.e., Google Earth and graphic calculator) and solved it using both the features of GeoGebra software and Desmos. In particular, the Activity Builder in Desmos, which is a unique strength of the program (DeGilio, 2022 ; McCulloch et al., 2018 ), enabled the PMTs to include and construct multiple learning opportunities for students (Chechan et al., 2023 ; Gulati, 2017 ). Additionally, constructing the problem in Desmos was easy and fun for the PMTs, as demonstrated by the teachers in McCulloch et al.’s ( 2018 ) study.

The PMTs used various digital technologies to design their modelling problem. It is obvious that their integration of pictures, and video-based and web-based (i.e. Google-earth) applications during warm-up activities supported the students in investigating the real-life context, as stated by Greefrath and Vos’ ( 2021 ) study. Specifically, the PMTs stated that watching the video and taking a 3D-tour in Google Earth could allow the students to explore, visualize, and incorporate the real-context for constructing both the real and mathematical models, as the students in Aytemiz and Çakmak Gürel’s study ( 2023 ). In the modelling problem, experimenting and exploring the problem context by using different sources could enable students to construct multiple solutions to the problem, which is due to the nature of the mathematical modelling.

After presenting the problem statement, the PMTs used different windows in Desmos to lead the students for solving the problem throughout the stages of the modelling cycle. Even though there is no linear direction in solving a mathematical modelling problem (Borromeo Ferri, 2007 ), designing a problem in Desmos could provide a direction for students in transition between different windows in Desmos, which also supported students in non-linear transition through modelling stages. In detail, by designing the problem in Desmos, the PMTs expected the students to make predictions regarding the context based on the data they collected during the warm-up activities. Additionally, the PMTs wanted students to construct a mathematical model using a graphic calculator, which supported them in creating graphs and operating on functions (McCulloch et al., 2018 ). While transforming from a mathematical solution to a real solution, the PMTs expected students to use a search-engine to investigate and formulate the required data for solving the problem based on their own interests (Borba et al., 2016 ; Villarreal et al., 2018 ), specifically in calculating the cost given in the problem. According to Blum and Leiß ( 2007 ), validation is defined as checking whether the predictions are reasonable and accurate. Existing studies acknowledge that the validation stage is the most challenging stage for students in solving a mathematical problem (Galbraith & Stillman, 2006 ). In this study, the PMTs provided an opportunity for students in the validation stage by constructing a window including a checklist in Desmos to compare their predictions with their mathematical results. In other words, the PMTs designed this problem by offering students the opportunity to predict, test, and explain their assumptions or solutions (Chorney, 2022 ).

While solving the problem, during transitioning from one stage to another, particular technological actions were revealed based on the PMTS’ aims of using different digital tools. In the transition from the real situation to both the situation and the real model, students must investigate and visualize the context. In particular, visualization allows the investigation of the real context. Additionally, visualization helped them investigate the necessary data in the images during the construction of the real model (Yiğit Koyunkaya & Tekin Dede, 2021 ). Therefore, the use of images integrated into GeoGebra and Desmos and web/video-based resources attracted students’ attention (Sinclair, 2003 , 2004 ) during the warm-up activities, and influenced them to visualize or imagine the real context. In other words, because the students had no experience with the real situation, the PMTs considered that the students were able to visualize the situation more clearly (Chamberlin & Moon, 2005 ). Therefore, they can initially construct the situation model and then the real model appropriately. This situation also supported the accuracy of the mathematical models that the students would construct in the following steps. In other words, using the features of GeoGebra (Greefrath et al., 2018 ) and Desmos (Chorney, 2022 ) supported both the PMTs (as well as the students) in visualizing the real context to make realistic assumptions for solving the problem.

While the PMTs constructed the possible mathematical models, they tested different quadratic equations that best represented the bridge by experimenting with different drawings. Greefrath and Siller ( 2017 , 2018 ) included the experimentalise action in working mathematically step, the PMTs provided evidence regarding the use of experiments for testing their assumptions and conditions by using the dynamic features in the simplifying step. After deciding to find the quadratic equation instead of using the circle arc, the PMTs used different technological actions. They constructed a slider to determine which quadratic equation best represented the bridge. In particular, they identified the coefficient in the equation by linking and dragging the point on the parabola (Arzarello et al., 2002 ). Even though initial models may be inadequate (Zawojewski, 2010 ), the PMTs’ decision to construct the slider and the dragging actions they used enabled them to verify the mathematical model to be the most appropriate to reality. Hence, their actions performed on GeoGebra triggered them to verify the mathematical model, as Greefrath ( 2011 ) stated. We also identified the action of verification in the interpretation step in which the real results were reconsidered. While Ramirez-Montes et al. ( 2021 ) stated that the digital tool could not support the interpretation step in their study, in contrast to this study, the PMTs provided evidence of using digital tools effectively at the interpretation step in our study. Another noteworthy result at this point is that comparing their results found in GeoGebra and Desmos triggered the PMTs to verify their real solutions. In terms of the modelling process, using digital tools in verification provided a validation of their real results as Schaap et al. ( 2011 ) stated. Borromeo Ferri ( 2006 ) described validation as knowledge-based and intuitive validation. In this study, the use of different digital tools allowed the PMTs to consciously use knowledge-based validation by using real data.

In their study, Greefrath ( 2011 ) and Greefrath et al. ( 2018 ) stated that constructing, drawing, measuring, visualizing, and controlling/verifying are possible technological actions that could be used in different modeling stages. In addition to their interpretations, our study provides evidence of possibilities for using different technological actions in the modelling cycle despite the small number of participants. To conclude, the integration of two different courses in the teacher education program revealed that the PMTs develop knowledge and experiences regarding the collaborative use of different contexts. This study could extend existing studies by providing opportunities as well as challenges to PMTs in designing and solving mathematical modelling problems using different digital tools, as Cevikbas et al. ( 2023 ) suggested. In this study, one group’s approaches in designing and solving a mathematical modelling problem helped extend Greefrath et al.’s ( 2018 ) framework; however, different actions could occur in different modelling stages while working with a larger number of participants as well as different mathematical modelling problems.

Data availability

The data analysed during this study are included in this article.

Through this paper, the definition of digital tools is accepted as digital media (e.g. computers, tablets, calculators, softwares, web 2.0 tools) used to support students’ learning specifically in mathematics lessons (Greefrath et al., 2018 ).

The Desmos link of the modelling problem named Festival in the City is as follows: https://teacher.desmos.com/activitybuilder/custom/65c21aa48e3a5be42f30577e .

https://www.youtube.com/watch?v=0tmvSBgvQTY

https://earth.google.com/web/@36.20002,36.1592417,85.74293325a,0d,60y,135.08378146h,85.4133161t,0r/data=Ii8KK0FGMVFpcE5hZjNkeXVmdFprUm11clhxTy13NEdmVUNVYnRJR1ZXQktJMTgQBToDCgEw

https://earth.google.com/web/@36.2000549,36.1590867,85.65766981a,0d,59.99999998y,330.47580843h,46.6211611t,0r/data=IjAKLEFGMVFpcFBzZTNjNlJRM2lNWFFSbXIwZ0VCWkhSd3R1eWs3US1KSGtnZ1FFEAU6AwoBMA

Arzarello, F., Ferrara, F., & Robutti, O. (2012). Mathematical modelling with technology: The role of dynamic representations. Teaching Mathematics and its Applications, 31 (1), 20–30. https://doi.org/10.1093/teamat/hrr027

Article Google Scholar

Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A cognitive analysis of dragging practises in Cabri environments. Zentralblatt für Didaktik Der Mathematik, 34 , 66–72. https://doi.org/10.1007/BF02655708

Aytemiz, H., & Çakmak Gürel, Z. (2023). Examining students’ mathematical modeling competences in video-based modeling tasks. The Journal of Educational Research, 116 (6), 336–348.

Blum, W., & Leiß, D. (2007). How do students and teachers deal with mathematical modelling problems? The example sugarloaf and the DISUM project. In C. Haines, P. L. Galbraith, W. Blum & S. Khan (Eds.), Mathematical modelling (ICTMA 12): Education, engineering and economics (pp. 222–231). Horwood. https://doi.org/10.1533/9780857099419.5.221

Borba, M. C., Askar, P., Engelbrecht, J., Gadanidis, G., Llinares, S., & Aguilar, M. S. (2016). Blended learning, e-learning and mobile learning in mathematics education. Zentralblatt für Didaktik der Mathematik-ZDM, 48 (5), 589–610.

Borromeo Ferri, R. (2006). Theoretical and empirical differentiations of phases in the modelling process. Zentralblatt für Didaktik der Mathematik-ZDM, 38 (2), 86–95.

Borromeo Ferri, R. (2007). Modelling problems from a cognitive perspective. In C. Haines, P. Galbraith, W. Blum, & S. Khan (Eds.), Mathematical modeling: Education, engineering, and economics (pp. 260–270). Woodhead Publishing Limited.

Google Scholar

Borromeo Ferri, R. (2018). Learning how to teach mathematical modeling in school and teacher education . Springer. https://doi.org/10.1007/978-3-319-68072-9

Bozkurt, G., & Ruthven, K. (2017). Classroom-based professional expertise: A mathematics teacher’s practice with technology. Educational Studies in Mathematics, 94 (3), 309–328.

Bozkurt, G., & Yigit Koyunkaya, M. (2022). Supporting prospective mathematics teachers’ planning and teaching technology-based tasks in the context of a practicum course. Teaching and Teacher Education, 119 , 103830. https://doi.org/10.1016/j.tate.2022.103830

Cevikbas, M., Greefrath, G., & Siller, H. S. (2023). Advantages and challenges of using digital technologies in mathematical modelling education – a descriptive systematic literature review. Frontiers in Education, 8 , 1–17. https://doi.org/10.3389/feduc.2023.1142556

Chamberlin, S. A., & Moon, S. M. (2005). Model eliciting activities as a tool to develop and identify creatively gifted mathematicians. Journal of Secondary Gifted Education, 17 (1), 37–47. https://doi.org/10.4219/jsge-2005-393

Chechan, B., Ampadu, E., & Pears, A. (2023). Effect of using desmos on high school students’ understanding and learning of functions. Eurasia Journal of Mathematics Science and Technology Education, 19 (10), em2331. https://doi.org/10.29333/ejmste/13540

Chorney, S. (2022). Classroom practice and craft knowledge in teaching mathematics using desmos: Challenges and strategies. International Journal of Mathematical Education in Science and Technology, 53 (12), 3203–3227. https://doi.org/10.1080/0020739X.2021.1931974

Article ADS Google Scholar

Clark-Wilson, A., Robutti, O., & Sinclair, N. (Eds.). (2014). The mathematics teacher in the digital era: An ınternational perspective on technology focused professional development. Springer. https://doi.org/10.1007/978-94-007-4638-1

Clark-Wilson, A., Robutti, O., & Sinclair, N. (Eds.). (2023). The mathematics teacher in the digital era: International research on professional learning and practice (2nd edn). Springer. https://doi.org/10.1007/978-3-031-05254-5

Confrey, J., & Maloney, A. (2007). A theory of mathematical modelling in technological settings. In W. Blum, P. L. Galbraith, H. W. Henn & M. Niss (Eds.), Modelling and applications in mathematics education. The 14th ICMI study (pp. 57–68). Springer. https://doi.org/10.1007/978-0-387-29822-1_4

Daher, W., & Shahbari, A. (2015). Pre-service teachers’ modelling processes through engagement with model eliciting activities with a technological tool. International Journal of Science and Mathematics Education, 13 , 25–46. https://doi.org/10.1007/s10763-013-9464-2

de Villiers, M. (1998). An alternative approach to proof in dynamic geometry. In R. Lehrer & D. Chazan (Eds.), Designing learning environments for developing understanding of geometry and space (pp. 369–393). Lawrence Erlbaum. https://doi.org/10.4324/9780203053461

DeGilio, M. (2022). Creating custom desmos activities using desmos activity builder to create effective lessons for online learning during Covid-19 . Master's thesis, SUNY Brockport.

English, L. D. (2016). STEM education K-12: Perspectives on integration. International Journal of STEM Education, 3 (1), 1–8. https://doi.org/10.1186/s40594-016-0036-1

Frassia, M. G., & Serpe, A. (2017). Learning geometry through mathematical modelling: An example with GeoGebra. TOJET: The Turkish Online Journal of Educational Technology, Special Issue for INTE 2017 (pp. 411–418)

Fuchs, K. J., & Blum, W. (2008). Selbständiges Lernen Im mathematikunterricht mit, beziehungsreichen‘ aufgaben. In J. Thonhauser (Ed.), Aufgaben als Katalysa- Toren Von Lernprozessen (pp. 135–147). Waxmann.

Galbraith, P., & Stillman, G. (2006). A framework for identifying student blockages during transitions in the modelling process. Zentralblatt für Didaktik Der Mathematik, 38 , 143–162. https://doi.org/10.1007/BF02655886

Geiger, V. (2011). Factors affecting teachers’ adoption of innovative practices with technology and mathematical modelling. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in Teaching and Learning of Mathematical Modelling: ICTMA14 (pp. 305–314). Springer. https://doi.org/10.1007/978-94-007-0910-2_31

Greefrath, G. (2011). Using technologies: New possibilities of teaching and learning modelling-Overview. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modelling, ICTMA 14 (pp. 301–304). Springer. https://doi.org/10.1007/978-94-007-0910-2_30

Greefrath, G., & Siller, H. S. (2017). Modelling and simulation with the help of digital tools. In G. A. Stillman, W. Blum, & G. Kaiser (Eds.), Mathematical modelling and applications, ICTMA 17 (pp. 529–539). Springer. https://doi.org/10.1007/978-3-319-62968-1_44

Greefrath, G., & Siller, H. S. (2018). GeoGebra as a tool in modelling processes. In L. Ball, P. Drijvers, S. Ladel, H. Siller, & M. Tabach (Eds.), Uses of technology in primary and secondary mathematics education (pp. 363–374). Springer. https://doi.org/10.1007/978-3-319-76575-4_21

Greefrath, G., & Vorhölter, K. (2016). Teaching and learning mathematical modelling: Approaches and developments from German speaking countries . Springer. https://doi.org/10.1007/978-3-319-45004-9

Greefrath, G. (2020). Mathematical modelling competence: Selected current research developments. Avances De Investigación en Educación Matemática, 17 , 38–51.

Greefrath, G., Hertleif, C., & Siller, H. S. (2018). Mathematical modelling with digital tools - a quantitative study on mathematising with dynamic geometry software. Zentralblatt für Didaktik Der Mathematik, 50 , 233–244. https://doi.org/10.1007/s11858-018-0924-6

Greefrath, G., Siller, H. S., & Weitendorf, J. (2011). Modelling considering the influence of technology. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillmann (Eds.), Trends in teaching and learning of mathematical modelling (pp. 315–329). Springer. https://doi.org/10.1007/978-94-007-0910-2_32

Greefrath, G., & Vos, P. (2021). Video-based word problems or modelling projects—Classifying ICT-based modelling tasks. In F. K. S. Leung, G. A. Stillman, G. Kaiser, & K. L. Wong (Eds.), Mathematical modelling education in east and west (pp. 489–499). Springer.

Chapter Google Scholar

Gulati, S. (2017). Create your own interactive activity. At Right Angles, 6 (3), 81–88.

Kaiser, G., Blomhøj, M., & Sriraman, B. (2006). Towards a didactical theory for mathematical modelling. Zentralblatt für Didaktik Der Mathematik, 38 (2), 82–85. https://doi.org/10.1007/BF02655882

Krippendorff, K. (1980). Validity in content analysis. In E. Mochmann (Ed.), Computerstrategien für die kommunikationsanalyse (pp. 69–112). Campus.

Laborde, C. (2001). Integration of technology in the design of geometry tasks with Cabri geometry. International Journal of Computers for Mathematical Learning, 6 , 283–317.

Lingefjaerd, T., et al. (2007). Modelling in teacher education. In W. Blum (Ed.), Modelling and applications in mathematics education (pp. 475–482). Springer.

Lingefjärd, T. (2000). Mathematical Modelling by Prospective Teachers using Technology . Doctoral dissertation. University of Georgia.

Lingefjärd, T. (2013). Teaching mathematical modelling in teacher education: Efforts and results. In X. S. Yang (Ed.), Mathematical modelling with multidisciplinary applications (pp. 57–80). John Wiley and Sons Inc.

Ludwig, M., & Jablonski, S. (2021). Step by step: Simplifying and mathematizing the real world with MathCityMap. Quadrante: Revista De Investigação em Educação Matemática, 30 (2), 242–268. https://doi.org/10.48489/quadrante.23604

McCulloch, A. W., Hollebrands, K., Lee, H., Harrison, T., & Mutlu, A. (2018). Factors that influence secondary mathematics teachers’ integration of technology in mathematics lessons. Computers & Education, 123 , 26–40. https://doi.org/10.1016/j.compedu.2018.04.008

Merriam, S. B. (1998). Qualitative research and case study applications in education (2nd ed.). Jossey-Bass.

Miles, M. B., & Huberman, A. M. (1994). Qualitative data analysis (2nd ed.). Sage.

Molina-Toro, J. F., Rendón-Mesa, P. A., & Villa-Ochoa, J. A. (2019). Research trends in digital technologies and modelling in mathematics education. Eurasia Journal of Mathematics Science and Technology Education, 15 (8), 1–13. https://doi.org/10.29333/ejmste/108438

Molina-Toro, J. F., Rendón-Mesa, P. A., & Villa-Ochoa, J. A. (2022). Contradictions in mathematical modelling with digital technologies. Education and Information Technologies, 27 , 1655–1673. https://doi.org/10.1007/s10639-021-10676-z

Patton, M. Q. (2014). Qualitative research and evaluation methods: Integrating theory and practice . Sage.

Ramírez-Montes, G., Carreira, S., & Henriques, A. (2021). Mathematical modelling routes supported by technology in the learning of linear algebra: A study with Costa Rican undergraduate students. Quadrante, 30 (1), 219–241.

Schaap, S., Vos, P., & Goedhart, M. (2011). Students overcoming blockages while building a mathematical model: Exploring a framework. In G. Kaiser, W. Blum, R. Borromeo Ferri, & G. Stillman (Eds.), Trends in teaching and learning of mathematical modeling (pp. 137–146). Springer.

Schukajlow, S., Kaiser, G., & Stillman, G. (2018). Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. Zentralblatt für Didaktik Der Mathematik, 50 , 5–18. https://doi.org/10.1007/s11858-018-0933-5

Siller, H. S., & Greefrath, G. (2010). Mathematical modelling in class regarding to technology. In V. Durand-Guerrier, S. Soury-Lavergne, & F. Arzarello (Eds.), Proceedings of the sixth congress of the European society for research in mathematics education(CERME6) (pp. 2136–2145). Institut National de Recherche Pédagogique.

Siller, H. S., Cevikbas, M., Geiger, V., & Greefrath, G. (2022). The role of digital resources in mathematical modelling research. In C. Fernández, S. Llinares, Á. Gutiérrez & N. Planas (Eds.), The Proceedings of 45th Conference of the International Group for the Psychology of Mathematics Education-PME , vol. 1 (pp. 152–155).

Sinclair, M. (2003). Some implications of the results of a case study for the design of pre constructed, dynamic geometry sketches and accompanying materials. Educational Studies in Mathematics, 52 (3), 289–317. https://doi.org/10.1023/A:1024305603330

Sinclair, M. (2004). Working with accurate representations: The case of pre-constructed dynamic geometry sketches. The Journal of Computers in Mathematics and Science Teaching, 23 (2), 191–208.

Stake, P. (2005). Qualitative case study. In N. K. Denzin & Y. S. Lincoln (Eds.), The sage handbook of qualitative research (pp. 433–466). Sage.

Tekin-Dede, A., & Bukova-Güzel, E. (2018). A rubric development study for the assessment of modeling skills. The Mathematics Educator, 27 (2), 33–72.

Villarreal, M. E., Esteley, C. B., & Smith, S. (2018). Pre-service teachers’ experiences within modelling scenarios enriched by digital technologies. Zentralblatt für Didaktik Der Mathematik, 50 , 327–341. https://doi.org/10.1007/s11858-018-0925-5

Viseu, F., & Leite, L. (2019). Developing technologically enhanced mathematics pedagogical content knowledge in initial teacher education. In L. Daniela (Ed.), Didactics of smart pedagogy (pp. 331–351). Springer. https://doi.org/10.1007/978-3-030-01551-0_17

Yiğit Koyunkaya, M., & Tekin Dede, A. (2021). Matematiksel modelleme problemlerinde teknoloji kullanımının rolü. In E. Bukova Güzel, M. F. Doğan, & A. Özaltun Çelik (Eds.), Matematiksel modelleme: Teoriden uygulamaya bütünsel bakış (pp. 295–320). Pegem Akademi.

Yin, R. K. (2018). Case study research: Design and methods (6th ed.). Sage.

Zawojewski, J. (2010). Problem solving versus modelling. In Lesh, R., Galbraith, P., Haines, C., Hurford, A. (Eds.), Modelling Students’ Mathematical Modelling Competencies (pp. 237–243). Springer. https://doi.org/10.1007/978-1-4419-0561-1_20

Download references

Open access funding provided by the Scientific and Technological Research Council of Türkiye (TÜBİTAK). No funding was received for conducting this study.

Author information

Authors and affiliations.

Buca Faculty of Education, Dokuz Eylül University, Buca, İzmir, Türkiye

Melike Yiğit Koyunkaya & Ayşe Tekin Dede

You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Melike Yiğit Koyunkaya .

Ethics declarations

Conflicts of interest.

The authors declare that there are no conflicts of interest or competing interests.

Additional information

Publisher’s note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Koyunkaya, M.Y., Dede, A.T. Using different digital tools in designing and solving mathematical modelling problems. Educ Inf Technol (2024). https://doi.org/10.1007/s10639-024-12577-3

Download citation

Received : 29 November 2023

Accepted : 14 February 2024

Published : 18 March 2024

DOI : https://doi.org/10.1007/s10639-024-12577-3

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

Digital tools
Technology integration in mathematics education
Mathematical modelling
Find a journal
Publish with us
Track your research

Along with Stanford news and stories, show me:

Student information
Faculty/Staff information

We want to provide announcements, events, leadership messages and resources that are relevant to you. Your selection is stored in a browser cookie which you can remove at any time using “Clear all personalization” below.

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start – to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics – a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced How to Learn Math , the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

In her new book, Math-ish: Finding Creativity, Diversity, and Meaning in Mathematics , Boaler argues for a broad, inclusive approach to math education, offering strategies and activities for learners at any age. We spoke with her about why creativity is an important part of mathematics, the impact of representing numbers visually and physically, and how what she calls “ishing” a math problem can help students make better sense of the answer.

What do you mean by “math-ish” thinking?

It’s a way of thinking about numbers in the real world, which are usually imprecise estimates. If someone asks how old you are, how warm it is outside, how long it takes to drive to the airport – these are generally answered with what I call “ish” numbers, and that’s very different from the way we use and learn numbers in school.

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 – but the most common answer 13-year-olds gave was 19. The second most common was 21.

I’m not surprised, because when students learn fractions, they often don’t learn to think conceptually or to consider the relationship between the numerator or denominator. They learn rules about creating common denominators and adding or subtracting the numerators, without making sense of the fraction as a whole. But stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a person can develop.

But don’t you also risk sending the message that mathematical precision isn’t important?

I’m not saying precision isn’t important. What I’m suggesting is that we ask students to estimate before they calculate, so when they come up with a precise answer, they’ll have a real sense for whether it makes sense. This also helps students learn how to move between big-picture and focused thinking, which are two different but equally important modes of reasoning.

Some people ask me, “Isn’t ‘ishing’ just estimating?” It is, but when we ask students to estimate, they often groan, thinking it’s yet another mathematical method. But when we ask them to “ish” a number, they're more willing to offer their thinking.

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mindset. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things – all of that contributes to our understanding of how it works.

There’s an activity we do with middle-school students where we show them an image of a 4 x 4 x 4 cm cube made up of smaller 1 cm cubes, like a Rubik’s Cube. The larger cube is dipped into a can of blue paint, and we ask the students, if they could take apart the little cubes, how many sides would be painted blue? Sometimes we give the students sugar cubes and have them physically build a larger 4 x 4 x 4 cube. This is an activity that leads into algebraic thinking.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, “I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.” His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing – elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

There’s an example in the book where you’ve asked students how they would calculate 38 x 5 in their heads, and they come up with several different ways of arriving at the same answer. The creativity is fascinating, but wouldn’t it be easier to teach students one standard method?

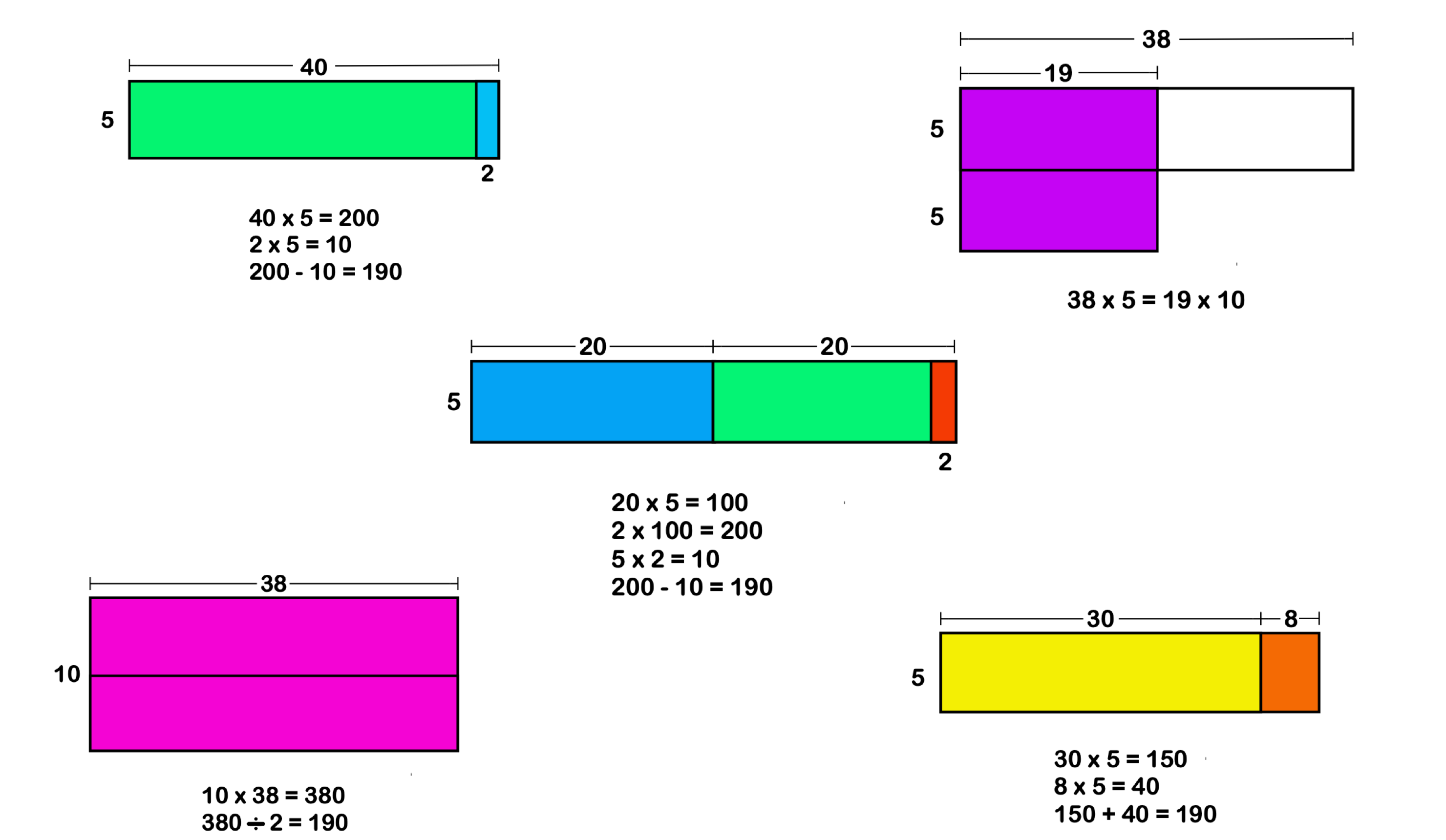
A depiction of various ways to calculate 38 x 5, numerically and visually. | Courtesy Jo Boaler

That narrow, rigid version of mathematics where there’s only one right approach is what most students experience, and it’s a big part of why people have such math trauma. It keeps them from realizing the full range and power of mathematics. When you only have students blindly memorizing math facts, they’re not developing number sense. They don’t learn how to use numbers flexibly in different situations. It also makes students who think differently believe there’s something wrong with them.

When we open mathematics to acknowledge the different ways a concept or problem can be viewed, we also open the subject to many more students. Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it’s powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.

{{subColumn.name}}

AIMS Mathematics

{{newsColumn.name}}
Share facebook twitter google linkedin

$set of problem solving tools in mathematics$

Modified mildly inertial subgradient extragradient method for solving pseudomonotone equilibrium problems and nonexpansive fixed point problems

Francis Akutsah 1 ,
Akindele Adebayo Mebawondu 1,2 , , ,
Austine Efut Ofem 1 ,
Reny George 3 , , ,
Hossam A. Nabwey 3,4 ,
Ojen Kumar Narain 1
1. School of Mathematics, Statistics and Computer Science, University of KwaZulu-Natal, Durban, South Africa
2. Mountain Top University, Prayer City, Ogun State Nigeria
3. Department of Mathematics, College of Science and Humanities in Al-Kharj, Prince Sattam Bin Abdulaziz University, Al-Kharj 11942, Saudi Arabia
4. Department of Basic Engineering, Faculty of Engineering, Menoufia University, Shibin el Kom 32511, Egypt
Received: 06 March 2024 Revised: 28 April 2024 Accepted: 09 May 2024 Published: 20 May 2024

MSC : 26A33, 34B10, 34B15

Full Text(HTML)
Download PDF

This paper presents and examines a newly improved linear technique for solving the equilibrium problem of a pseudomonotone operator and the fixed point problem of a nonexpansive mapping within a real Hilbert space framework. The technique relies two modified mildly inertial methods and the subgradient extragradient approach. In addition, it can be viewed as an advancement over the previously known inertial subgradient extragradient approach. Based on common assumptions, the algorithm's weak convergence has been established. Finally, in order to confirm the efficiency and benefit of the proposed algorithm, we present a few numerical experiments.

subgradient extragradient ,
mildly inertial ,
equilibrium problem ,
fixed point problem

Citation: Francis Akutsah, Akindele Adebayo Mebawondu, Austine Efut Ofem, Reny George, Hossam A. Nabwey, Ojen Kumar Narain. Modified mildly inertial subgradient extragradient method for solving pseudomonotone equilibrium problems and nonexpansive fixed point problems[J]. AIMS Mathematics, 2024, 9(7): 17276-17290. doi: 10.3934/math.2024839

Supplements

Access history.

Corresponding authors: Email: [email protected] ; Email: [email protected] ;

Reader Comments

© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院沈阳 110142

$set of problem solving tools in mathematics$

Article views( 76 ) PDF downloads( 12 ) Cited by( 0 )

Figures and Tables

$set of problem solving tools in mathematics$

Figures( 2 ) / Tables( 2 )

Associated material

Export File

Figure 1. Example 1, Case A (top left); Case B (top right); Case C (bottom left); Case D (bottom right)
Figure 2. Example 2, Case I (top left); Case II (top right); Case III (bottom left); Case IV (bottom right)

Future Students
Current Students
Faculty/Staff

News and Media

News & Media Home
Research Stories
School's In
In the Media

For everyone whose relationship with mathematics is distant or broken, Jo Boaler , a professor at Stanford Graduate School of Education (GSE), has ideas for repairing it. She particularly wants young people to feel comfortable with numbers from the start — to approach the subject with playfulness and curiosity, not anxiety or dread.

“Most people have only ever experienced what I call narrow mathematics — a set of procedures they need to follow, at speed,” Boaler says. “Mathematics should be flexible, conceptual, a place where we play with ideas and make connections. If we open it up and invite more creativity, more diverse thinking, we can completely transform the experience.”

“Mathematics should be flexible, conceptual, a place where we play with ideas and make connections," says Professor Jo Boaler. (Photo: Robert Houser Photography)

Boaler, the Nomellini and Olivier Professor of Education at the GSE, is the co-founder and faculty director of Youcubed , a Stanford research center that provides resources for math learning that has reached more than 230 million students in over 140 countries. In 2013 Boaler, a former high school math teacher, produced “How to Learn Math,” the first massive open online course (MOOC) on mathematics education. She leads workshops and leadership summits for teachers and administrators, and her online courses have been taken by over a million users.

What do you mean by “math-ish” thinking?

In the book I share an example of a multiple-choice question from a nationwide exam where students are asked to estimate the sum of two fractions: 12/13 + 7/8. They’re given four choices for the closest answer: 1, 2, 19, or 21. Each of the fractions in the question is very close to 1, so the answer would be 2 — but the most common answer 13-year-olds gave was 19. The second most common was 21.

But don’t you also risk sending the message that mathematical precision isn’t important?

Ishing helps students develop a sense for numbers and shapes. It can help soften the sharp edges in mathematics, making it easier for kids to jump in and engage. It can buffer students against the dangers of perfectionism, which we know can be a damaging mind-set. I think we all need a little more ish in our lives.

You also argue that mathematics should be taught in more visual ways. What do you mean by that?

For most people, mathematics is an almost entirely symbolic, numerical experience. Any visuals are usually sterile images in a textbook, showing bisecting angles, or circles divided into slices. But the way we function in life is by developing models of things in our minds. Take a stapler: Knowing what it looks like, what it feels and sounds like, how to interact with it, how it changes things — all of that contributes to our understanding of how it works.

Some years back we were interviewing students a year after they’d done that activity in our summer camp and asked what had stayed with them. One student said, ‘I’m in geometry class now, and I still remember that sugar cube, what it looked like and felt like.’ His class had been asked to estimate the volume of their shoes, and he said he’d imagined his shoes filled with 1 cm sugar cubes in order to solve that question. He had built a mental model of a cube.

When we learn about cubes, most of us don’t get to see and manipulate them. When we learn about square roots, we don’t take squares and look at their diagonals. We just manipulate numbers.

I wonder if people consider the physical representations more appropriate for younger kids.

That’s the thing — elementary school teachers are amazing at giving kids those experiences, but it dies out in middle school, and by high school it’s all symbolic. There’s a myth that there’s a hierarchy of sophistication where you start out with visual and physical representations and then build up to the symbolic. But so much of high-level mathematical work now is visual. Here in Silicon Valley, if you look at Tesla engineers, they're drawing, they're sketching, they're building models, and nobody says that's elementary mathematics.

Visualization of different ways to calculate 38 times 5

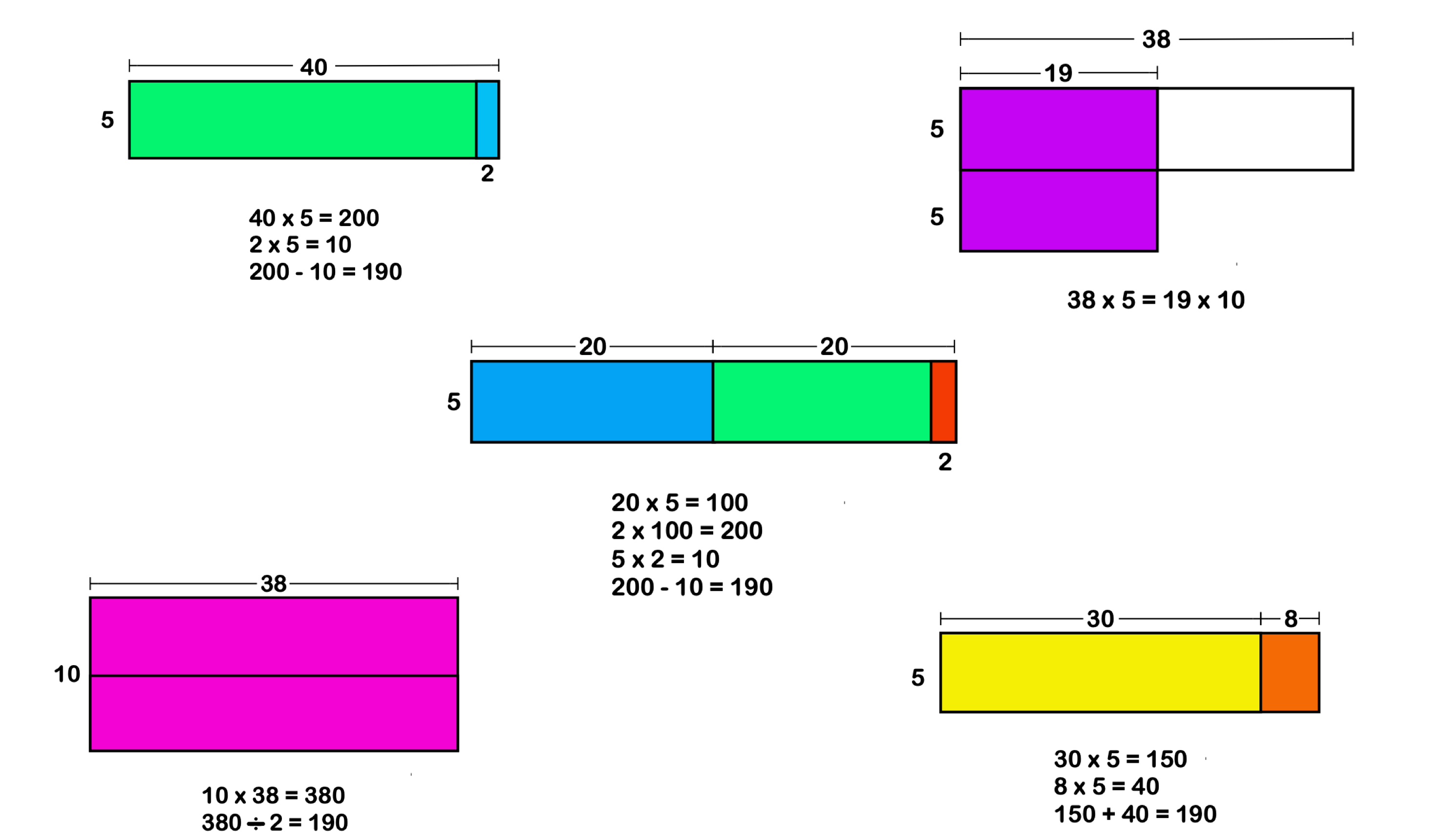
Click to enlarge: A depiction of various ways to calculate 38 x 5, numerically and visually. (Image: Courtesy of Jo Boaler)

Get the Educator

Subscribe to our monthly newsletter.

Stanford Graduate School of Education

482 Galvez Mall Stanford, CA 94305-3096 Tel: (650) 723-2109

Contact Admissions
GSE Leadership
Site Feedback
Web Accessibility
Career Resources
Faculty Open Positions
Explore Courses
Academic Calendar
Office of the Registrar
Cubberley Library
StanfordWho
StanfordYou

Improving lives through learning

Stanford Home
Maps & Directions
Search Stanford
Emergency Info
Terms of Use
Non-Discrimination
Accessibility

IMAGES

Problem Solving Strategies for Math Poster by TeachPlanLove
$set of problem solving tools in mathematics$
18 Math Problem Solving Tools
$set of problem solving tools in mathematics$
The Math Problem Solving Toolbox
$set of problem solving tools in mathematics$
example of a problem solving tool
Problem Solving Infographic 10 Steps Concept Vector Image
Problem Solving Steps Math

VIDEO

Problem Solving tools -part2
Problem Solving Lesson #5
Introduction to the 7 Problem Solving Tools
Problem Solving
Problem Solving
Solving Three Set Problems

COMMENTS

20 Effective Math Strategies For Problem Solving
Here are five strategies to help students check their solutions. 1. Use the Inverse Operation. For simpler problems, a quick and easy problem solving strategy is to use the inverse operation. For example, if the operation to solve a word problem is 56 ÷ 8 = 7 students can check the answer is correct by multiplying 8 × 7.
Module 1: Problem Solving Strategies
Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
GeoGebra Math Solver
Download our apps here: English / English (United States) Get accurate solutions and step-by-step explanations for algebra and other math problems with the free GeoGebra Math Solver. Enhance your problem-solving skills while learning how to solve equations on your own. Try it now!
1.5: Problem Solving
Solution. Step 1: Understanding the problem. We are given in the problem that there are 25 chickens and cows. All together there are 76 feet. Chickens have 2 feet and cows have 4 feet. We are trying to determine how many cows and how many chickens Mr. Jones has on his farm. Step 2: Devise a plan.
Mathematics Through Problem Solving
A further characteristic is that a problem-solving approach can be used to encourage students to make generalisations about rules and concepts, a process which is central to mathematics (Evan and Lappin, 1994). Schoenfeld (in Olkin and Schoenfeld, 1994, p.43) described the way in which the use of problem solving in his teaching has changed ...
Microsoft Math Solver
Get math help in your language. Works in Spanish, Hindi, German, and more. Online math solver with free step by step solutions to algebra, calculus, and other math problems. Get help on the web or with our math app.
1.3: Problem Solving Strategies
Problem Solving Strategy 3 (Draw a Picture). Some problems are obviously about a geometric situation, and it is clear you want to draw a picture and mark down all of the given information before you try to solve it. But even for a problem that is not geometric, like this one, thinking visually can help!
Mathway
Free math problem solver answers your algebra homework questions with step-by-step explanations.
Step-by-Step Calculator
To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
Step-by-Step Math Problem Solver
QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students. The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and ...
Problem-Solving in Mathematics Education
Introduction. Problem-solving approaches appear in all human endeavors. In mathematics, activities such as posing or defining problems and looking for different ways to solve them are central to the development of the discipline. In mathematics education, the systematic study of what the process of formulating and solving problems entails and ...
Mathigon
The Mathematical Playground. Free tools, courses and manipulatives to make online learning more interactive and engaging than ever before. ... Our unparalleled interactivity allow students to explore, discover, learn problem-solving and be creative. Captivating storytelling and real applications make abstract topics more engaging than ever ...
PDF Problem solving in mathematics
Therefore, high-quality assessment of problem solving in public tests and assessments1 is essential in order to ensure the effective learning and teaching of problem solving throughout primary and secondary education. Although the focus here is on the assessment of problem solving in mathematics, many of the ideas will be directly transferable ...
Mathematics as a Complex Problem-Solving Activity
A problem in mathematics is any situation that must be resolved using mathematical tools but for which there is no immediately obvious strategy. ... rather than remembering and applying a set of procedures. It is through problem-solving that students develop a deeper understanding of mathematical concepts, become more engaged, and appreciate ...
10 Best Math AI Solvers to Solve Math Problems Online
It is also highly effective at solving math word problems with step-by-step solutions. With Interactive Mathematics, users can type in their math problems or copy and paste a photo. The tool then analyzes the problem and delivers near-instant results. Pros: Efficient at solving math word problems. Optimized for mobile phones and tablet use.
List of Top 13 Math Software to Solve Math Problem Efficiently
Powerful scanning and solving. Sketch Calculator. Microsoft Mathematics Pricing: Microsoft Math Solver is a free software for mathematics. Microsoft Math Solver Compatibility: Users can download and install it in Windows 8 and above. Besides, you can also use the math software online through Edge browser.
Sets
Consider the same example above. If the element 4 4 is removed from the set B B, solve for (i), (ii), (iii) as well. (i) Since there is no common elements in sets A A and B B, then A \cap B = \phi A∩B = ϕ or A \cap B = \ { \} A∩B = {}. (ii) Because the element 4 4 is no longer repeated, then A \cup B A ∪B remains the same.
Engaging Students in Mathematical Problem Solving with Technology
Studying the use and impact of digital tools on mathematical problem solving requires an examination of how interactions between individuals ... While there are other initiatives that involve similar content or aim to promote a somewhat similar set of skills, such as mathematical problem-solving competitions (e.g., Olympiads) or technology ...
1.1: Introduction to Problem Solving
The very first Mathematical Practice is: Make sense of problems and persevere in solving them. Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They analyze givens, constraints, relationships, and goals. They make conjectures about the form and meaning of ...
35 problem-solving techniques and methods for solving complex problems
The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we've given you the tools to find the best solutions as simply and easily as possible.
Problem solving
Problem solving is the process of achieving a goal by overcoming obstacles, a frequent part of most activities. Problems in need of solutions habit from simple personal tasks (e.g. how to turn on an appliance) to complex issues in business and technical fields. The former is an example of simple problem solving (SPS) addressing one issue ...
Identification of Problem-Solving Techniques in Computational Thinking
Problem solving (PS), a component of critical thinking (Chaisri et al., 2019; Kuo et al., 2020), is a form of human intelligence that uses a structural phase to find an unknown or developing answer (Jones-Harris & Chamblee, 2017; Polya, 1981); PS organizes thoughts and processes to find a solution.Problem solving is a human skill that is required to deal with the complexity of problems (Durak ...
Using different digital tools in designing and solving mathematical
According to Blum and Leiß's cycle, first students understand a real-life problem and construct a situation model explaining the problem.Then, they simplify the situation model and construct the real model by making the necessary assumptions. During the mathematization process, students construct mathematical models and then obtain mathematical results by solving the models.
PDF MATHEMATICAL PROBLEM-SOLVING STRATEGIES AMONG STUDENT TEACHERS
Techniques and analytical tools by Strauss and Corbin (1998) and the constant comparison method by Glaser and Strauss (1967) were used. The data used in the study ... The student teachers answered the given set of problem-solving and the Mathematics Motivated Strategies Learning Questionnaires. The outputs of the students in the
Teaching mathematics as a tool for problem-solving
Teaching mathematics as a tool for problem-solving - UNESCO ... article
The case for 'math-ish' thinking
<p>In a new book, Jo Boaler argues for a more flexible, creative approach to math. "Stepping back and judging whether a calculation is reasonable might be the most valuable mathematical skill a ...
Math Message Boards FAQ & Community Help
math training & tools Alcumus ... just for fun Reaper Greed Control. view all 0. Sign In. Register. Avoid summer slump with our math, science, competition training, and computer science courses - schedule today! Community. Art of Problem Solving is an ACS WASC Accredited School . aops programs. AoPS Online. Beast Academy. AoPS Academy. About ...
Modified mildly inertial subgradient extragradient method for solving
<abstract> This paper presents and examines a newly improved linear technique for solving the equilibrium problem of a pseudomonotone operator and the fixed point problem of a nonexpansive mapping within a real Hilbert space framework. The technique relies two modified mildly inertial methods and the subgradient extragradient approach. In addition, it can be viewed as an advancement over the ...
Softening the sharp edges in mathematics
Mathematical diversity, to me, is a concept that includes both the value of diversity in people and the diverse ways we can see and learn mathematics. When we bring those forms of diversity together, it's powerful. If we want to value different ways of thinking and problem-solving in the world, we need to embrace mathematical diversity.
The Proven Tool To Level Up Your (And Your Team's ...
Approach challenges with a strategically focused problem-solving mindset — bringing multiple solutions to the table rather than solely seeking answers. Approach challenges with an open mind and ...

20 Effective Math Strategies To Approach Problem-Solving

What are problem-solving strategies?

20 Math Strategies For Problem-Solving

Strategies to understand the problem

1. Read the problem aloud

2. Highlight keywords

3. Summarize the information

4. Determine the unknown

5. Make a plan

Strategies for solving the problem

2. Act it out

3. Work backwards

4. Write a number sentence

5. Use a formula

Strategies for checking the solution

1. Use the Inverse Operation

2. Estimate to check for reasonableness

3. Plug-In Method

4. Peer Review

5. Use a Calculator

Step-by-step problem-solving processes for your classroom

How Third Space Learning improves problem-solving

One-on-one tutoring

Problem-solving

Related articles

Ultimate Guide to Metacognition [FREE]

Privacy Overview

Math Solver

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Solver Title

Generating PDF...

Most Used Actions

What can QuickMath do?

Math Topics

Mathematics as a Complex Problem-Solving Activity

Learning to problem solve

Beliefs underpinning effective teaching of mathematics

Why is problem-solving important?

Problems that are “Problematic”

Pólya’s Principals of Problem-Solving

Getting real

Planning for talk

10 Best Math AI Solvers to Solve Math Problems Online

Mathful – Best Overall Math AI Solver to Solve Math Problems

AI Math – Best AI Math Solver for All Grade Levels

HIX Tutor – Best AI Math Solver for High Accuracy

HomeworkAI – Best All-in-One Solution for Homework Help

Question AI – Best Homework AI Tool for Greater Academic Success

QuickMath – Best Math AI Solver for High School and College Students

Smodin – Best AI Math Solver for Acing Math Exams

StudyMonkey – Best AI Math Problem Solver for Personalized Learning

Interactive Mathematics – Best Math AI Tool for Solving Word Problems

SnapXam – Best AI Math Solver for On-the-Go

Please Login to comment...

What kind of Experience do you want to share?

List of Top 13 Math Software to Solve Math Problem Efficiently

Best Math Software for Teachers, Students, and Engineers

Best Math Software for Students

Best Math Software for Teachers

Open Source and Free Math Software

Math Software for Engineers and Researchers

Which software is best for mathematics?

What is the best free Math software?

What is the best Math software for PC?

What is the best Math software for Mac?

Sets - Problem Solving

This wiki is incomplete.

Bonus question given with the picture.

Margin Size

1.1: Introduction to Problem Solving

Think / Pair / Share

Problem Solving Strategy 1 (Wishful Thinking).

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Recommended Articles

How do you identify problems?