formula of de broglie hypothesis

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

6.6: De Broglie’s Matter Waves

Last updated
Save as PDF
Page ID 4524

Learning Objectives

By the end of this section, you will be able to:

Describe de Broglie’s hypothesis of matter waves
Explain how the de Broglie’s hypothesis gives the rationale for the quantization of angular momentum in Bohr’s quantum theory of the hydrogen atom
Describe the Davisson–Germer experiment
Interpret de Broglie’s idea of matter waves and how they account for electron diffraction phenomena

Compton’s formula established that an electromagnetic wave can behave like a particle of light when interacting with matter. In 1924, Louis de Broglie proposed a new speculative hypothesis that electrons and other particles of matter can behave like waves. Today, this idea is known as de Broglie’s hypothesis of matter waves . In 1926, De Broglie’s hypothesis, together with Bohr’s early quantum theory, led to the development of a new theory of wave quantum mechanics to describe the physics of atoms and subatomic particles. Quantum mechanics has paved the way for new engineering inventions and technologies, such as the laser and magnetic resonance imaging (MRI). These new technologies drive discoveries in other sciences such as biology and chemistry.

According to de Broglie’s hypothesis, massless photons as well as massive particles must satisfy one common set of relations that connect the energy $E$ with the frequency $f$, and the linear momentum $p$ with the wavelength $λ$. We have discussed these relations for photons in the context of Compton’s effect. We are recalling them now in a more general context. Any particle that has energy and momentum is a de Broglie wave of frequency $f$ and wavelength $\lambda$:

\[ E = h f \label{6.53} \]

\[ \lambda = \frac{h}{p} \label{6.54} \]

Here, $E$ and $p$ are, respectively, the relativistic energy and the momentum of a particle. De Broglie’s relations are usually expressed in terms of the wave vector $\vec{k}$, $k = 2 \pi / \lambda$, and the wave frequency $\omega = 2 \pi f$, as we usually do for waves:

\begin{aligned} &E=\hbar \omega \label{6.55}\\ &\vec{p}=\hbar \vec{k} \label{6.56} \end{aligned}

Wave theory tells us that a wave carries its energy with the group velocity . For matter waves, this group velocity is the velocity $u$ of the particle. Identifying the energy E and momentum p of a particle with its relativistic energy $mc^2$ and its relativistic momentum $mu$, respectively, it follows from de Broglie relations that matter waves satisfy the following relation:

\[ \lambda f =\frac{\omega}{k}=\frac{E / \hbar}{p / \hbar}=\frac{E}{p} = \frac{m c^{2}}{m u}=\frac{c^{2}}{u}=\frac{c}{\beta} \label{6.57} \]

where $\beta = u/c$. When a particle is massless we have $u=c$ and Equation \ref{6.57} becomes $\lambda f = c$.

Example $\PageIndex{1}$: How Long are de Broglie Matter Waves?

Calculate the de Broglie wavelength of:

a 0.65-kg basketball thrown at a speed of 10 m/s,
a nonrelativistic electron with a kinetic energy of 1.0 eV, and
a relativistic electron with a kinetic energy of 108 keV.

We use Equation \ref{6.57} to find the de Broglie wavelength. When the problem involves a nonrelativistic object moving with a nonrelativistic speed u , such as in (a) when $\beta=u / c \ll 1$, we use nonrelativistic momentum p . When the nonrelativistic approximation cannot be used, such as in (c), we must use the relativistic momentum $p=m u=m_{0} \gamma u=E_{0} \gamma \beta/c$, where the rest mass energy of a particle is $E_0 = m c^2 $ and $\gamma$ is the Lorentz factor $\gamma=1 / \sqrt{1-\beta^{2}}$. The total energy $E$ of a particle is given by Equation \ref{6.53} and the kinetic energy is $K=E-E_{0}=(\gamma-1) E_{0}$. When the kinetic energy is known, we can invert Equation 6.4.2 to find the momentum

\[ p=\sqrt{\left(E^{2}-E_{0}^{2}\right) / c^{2}}=\sqrt{K\left(K+2 E_{0}\right)} / c \nonumber \]

and substitute into Equation \ref{6.57} to obtain

\[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}} \label{6.58} \]

Depending on the problem at hand, in this equation we can use the following values for hc :

\[ h c=\left(6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}\right)\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)=1.986 \times 10^{-25} \: \mathrm{J} \cdot \mathrm{m}=1.241 \: \mathrm{eV} \cdot \mu \mathrm{m} \nonumber \]

For the basketball, the kinetic energy is \[ K=m u^{2} / 2=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})^{2} / 2=32.5 \: \mathrm{J} \nonumber \] and the rest mass energy is \[ E_{0}=m c^{2}=(0.65 \: \mathrm{kg})\left(2.998 \times 10^{8} \: \mathrm{m} / \mathrm{s}\right)^{2}=5.84 \times 10^{16} \: \mathrm{J} \nonumber \] We see that $K /\left(K+E_{0}\right) \ll 1$ and use $p=m u=(0.65 \: \mathrm{kg})(10 \: \mathrm{m} / \mathrm{s})=6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m} $: \[ \lambda=\frac{h}{p}=\frac{6.626 \times 10^{-34} \: \mathrm{J} \cdot \mathrm{s}}{6.5 \: \mathrm{J} \cdot \mathrm{s} / \mathrm{m}}=1.02 \times 10^{-34} \: \mathrm{m} \nonumber \]
For the nonrelativistic electron, \[ E_{0}=mc^{2}=\left(9.109 \times 10^{-31} \mathrm{kg}\right)\left(2.998 \times 10^{8} \mathrm{m} / \mathrm{s}\right)^{2}=511 \mathrm{keV} \nonumber \] and when $K = 1.0 \: eV$, we have $K/(K+E_0) = (1/512) \times 10^{-3} \ll 1$, so we can use the nonrelativistic formula. However, it is simpler here to use Equation \ref{6.58}: \[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{(1.0 \: \mathrm{eV})[1.0 \: \mathrm{eV}+2(511 \: \mathrm{keV})]}}=1.23 \: \mathrm{nm} \nonumber \] If we use nonrelativistic momentum, we obtain the same result because 1 eV is much smaller than the rest mass of the electron.
For a fast electron with $K=108 \: keV$, relativistic effects cannot be neglected because its total energy is $E = K = E_0 = 108 \: keV + 511 \: keV = 619 \: keV$ and $K/E = 108/619$ is not negligible: \[ \lambda=\frac{h}{p}=\frac{h c}{\sqrt{K\left(K+2 E_{0}\right)}}=\frac{1.241 \: \mathrm{eV} \cdot \mu \mathrm{m}}{\sqrt{108 \: \mathrm{keV}[108 \: \mathrm{keV}+2(511 \: \mathrm{keV})]}}=3.55 \: \mathrm{pm} \nonumber \].

Significance

We see from these estimates that De Broglie’s wavelengths of macroscopic objects such as a ball are immeasurably small. Therefore, even if they exist, they are not detectable and do not affect the motion of macroscopic objects.

Exercise $\PageIndex{1}$

What is de Broglie’s wavelength of a nonrelativistic proton with a kinetic energy of 1.0 eV?

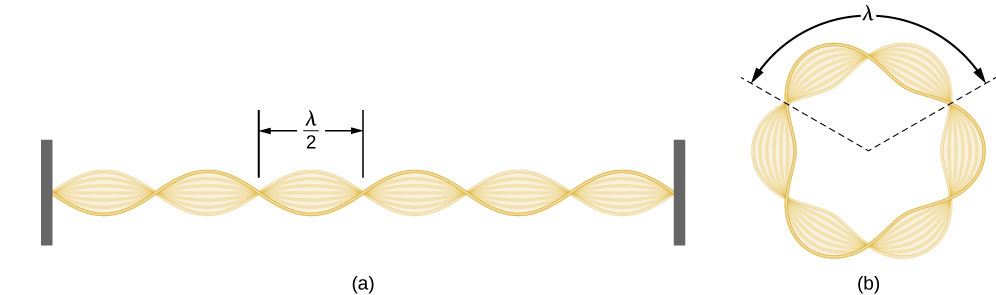
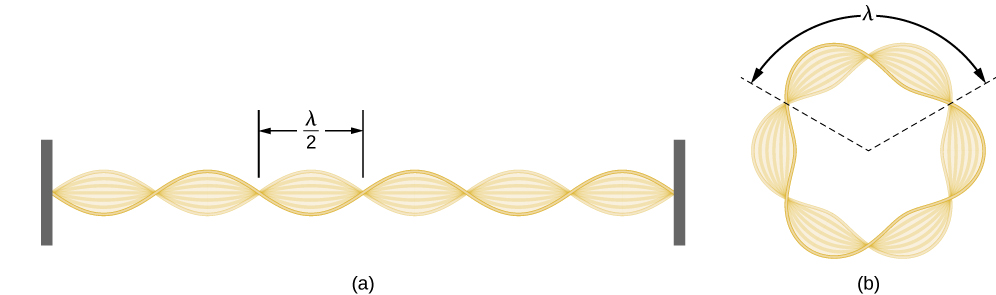
Using the concept of the electron matter wave, de Broglie provided a rationale for the quantization of the electron’s angular momentum in the hydrogen atom, which was postulated in Bohr’s quantum theory. The physical explanation for the first Bohr quantization condition comes naturally when we assume that an electron in a hydrogen atom behaves not like a particle but like a wave. To see it clearly, imagine a stretched guitar string that is clamped at both ends and vibrates in one of its normal modes. If the length of the string is l (Figure $\PageIndex{1}$), the wavelengths of these vibrations cannot be arbitrary but must be such that an integer k number of half-wavelengths $\lambda/2$ fit exactly on the distance l between the ends. This is the condition $l=k \lambda /2$ for a standing wave on a string. Now suppose that instead of having the string clamped at the walls, we bend its length into a circle and fasten its ends to each other. This produces a circular string that vibrates in normal modes, satisfying the same standing-wave condition, but the number of half-wavelengths must now be an even number $k$, $k=2n$, and the length l is now connected to the radius $r_n$ of the circle. This means that the radii are not arbitrary but must satisfy the following standing-wave condition:

\[ 2 \pi r_{n}=2 n \frac{\lambda}{2} \label{6.59}. \]

If an electron in the n th Bohr orbit moves as a wave, by Equation \ref{6.59} its wavelength must be equal to $\lambda = 2 \pi r_n / n$. Assuming that Equation \ref{6.58} is valid, the electron wave of this wavelength corresponds to the electron’s linear momentum, $p = h/\lambda = nh / (2 \pi r_n) = n \hbar /r_n$. In a circular orbit, therefore, the electron’s angular momentum must be

\[ L_{n}=r_{n} p=r_{n} \frac{n \hbar}{r_{n}}=n \hbar \label{6.60} . \]

This equation is the first of Bohr’s quantization conditions, given by Equation 6.5.6 . Providing a physical explanation for Bohr’s quantization condition is a convincing theoretical argument for the existence of matter waves.

Figure A is the standing-wave pattern for a string clamped in the wall. The distance between each node corresponds to the half gamma. Figure B is the standing-wave pattern for an electron wave trapped in the third Bohr orbit in the hydrogen atom. The wave has a circular shape with six nodes. The distance between each two node corresponds to the gamma.

Example $\PageIndex{2}$: The Electron Wave in the Ground State of Hydrogen

Find the de Broglie wavelength of an electron in the ground state of hydrogen.

We combine the first quantization condition in Equation \ref{6.60} with Equation 6.5.6 and use Equation 6.5.9 for the first Bohr radius with $n = 1$.

When $n=1$ and $r_n = a_0 = 0.529 \: Å$, the Bohr quantization condition gives $a_{0} p=1 \cdot \hbar \Rightarrow p=\hbar / a_{0}$. The electron wavelength is:

\[ \lambda=h / p = h / \hbar / a_{0} = 2 \pi a_{0} = 2 \pi(0.529 \: Å)=3.324 \: Å .\nonumber \]

We obtain the same result when we use Equation \ref{6.58} directly.

Exercise $\PageIndex{2}$

Find the de Broglie wavelength of an electron in the third excited state of hydrogen.

$\lambda = 2 \pi n a_0 = 2 (3.324 \: Å) = 6.648 \: Å$

Experimental confirmation of matter waves came in 1927 when C. Davisson and L. Germer performed a series of electron-scattering experiments that clearly showed that electrons do behave like waves. Davisson and Germer did not set up their experiment to confirm de Broglie’s hypothesis: The confirmation came as a byproduct of their routine experimental studies of metal surfaces under electron bombardment.

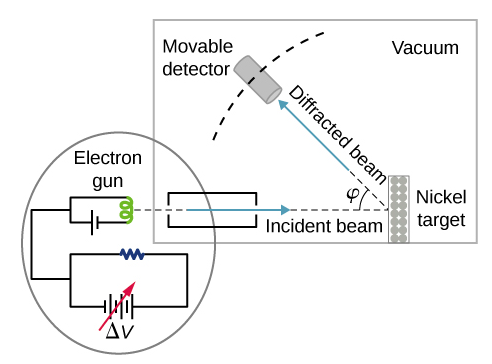
In the particular experiment that provided the very first evidence of electron waves (known today as the Davisson–Germer experiment ), they studied a surface of nickel. Their nickel sample was specially prepared in a high-temperature oven to change its usual polycrystalline structure to a form in which large single-crystal domains occupy the volume. Figure $\PageIndex{2}$ shows the experimental setup. Thermal electrons are released from a heated element (usually made of tungsten) in the electron gun and accelerated through a potential difference ΔV, becoming a well-collimated beam of electrons produced by an electron gun. The kinetic energy $K$ of the electrons is adjusted by selecting a value of the potential difference in the electron gun. This produces a beam of electrons with a set value of linear momentum, in accordance with the conservation of energy:

\[ e \Delta V=K=\frac{p^{2}}{2 m} \Rightarrow p=\sqrt{2 m e \Delta V} \label{6.61} \]

The electron beam is incident on the nickel sample in the direction normal to its surface. At the surface, it scatters in various directions. The intensity of the beam scattered in a selected direction φφ is measured by a highly sensitive detector. The detector’s angular position with respect to the direction of the incident beam can be varied from φ=0° to φ=90°. The entire setup is enclosed in a vacuum chamber to prevent electron collisions with air molecules, as such thermal collisions would change the electrons’ kinetic energy and are not desirable.

$Figure shows the schematics of the experimental setup of the Davisson–Germer diffraction experiment. A beam of electrons is emitted by the electron gun, passes through the collimator, and hits Nickel target. Diffracted beam forms an angle phi with the incident beam and is detected by a moving detector. All of this is shown happening in a vacuum$

When the nickel target has a polycrystalline form with many randomly oriented microscopic crystals, the incident electrons scatter off its surface in various random directions. As a result, the intensity of the scattered electron beam is much the same in any direction, resembling a diffuse reflection of light from a porous surface. However, when the nickel target has a regular crystalline structure, the intensity of the scattered electron beam shows a clear maximum at a specific angle and the results show a clear diffraction pattern (see Figure $\PageIndex{3}$). Similar diffraction patterns formed by X-rays scattered by various crystalline solids were studied in 1912 by father-and-son physicists William H. Bragg and William L. Bragg. The Bragg law in X-ray crystallography provides a connection between the wavelength $\lambda$ of the radiation incident on a crystalline lattice, the lattice spacing, and the position of the interference maximum in the diffracted radiation (see Diffraction ).

The graph shows the dependence of the intensity of the scattering beam on the scattering angle in degrees. The intensity degrees from 10 to 30 degrees, followed by a sharp increase and maximum at 50 degrees, and then reaches zero at 80 degrees.

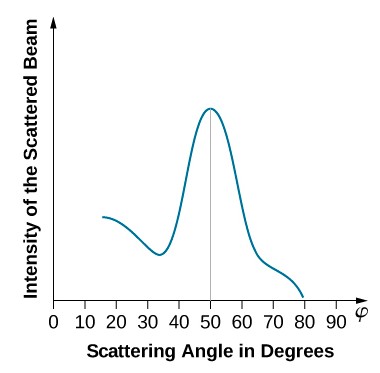
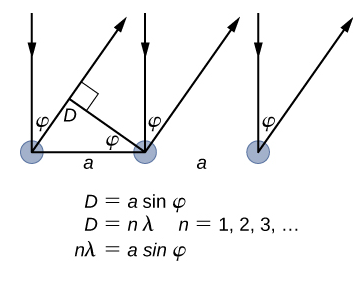
The lattice spacing of the Davisson–Germer target, determined with X-ray crystallography, was measured to be $a=2.15 \: Å$. Unlike X-ray crystallography in which X-rays penetrate the sample, in the original Davisson–Germer experiment, only the surface atoms interact with the incident electron beam. For the surface diffraction, the maximum intensity of the reflected electron beam is observed for scattering angles that satisfy the condition nλ = a sin φ (see Figure $\PageIndex{4}$). The first-order maximum (for n=1) is measured at a scattering angle of φ≈50° at ΔV≈54 V, which gives the wavelength of the incident radiation as λ=(2.15 Å) sin 50° = 1.64 Å. On the other hand, a 54-V potential accelerates the incident electrons to kinetic energies of K = 54 eV. Their momentum, calculated from Equation \ref{6.61}, is $p = 2.478 \times 10^{−5} \: eV \cdot s/m$. When we substitute this result in Equation \ref{6.58}, the de Broglie wavelength is obtained as

\[ \lambda=\frac{h}{p}=\frac{4.136 \times 10^{-15} \mathrm{eV} \cdot \mathrm{s}}{2.478 \times 10^{-5} \mathrm{eV} \cdot \mathrm{s} / \mathrm{m}}=1.67 \mathrm{Å} \label{6.62}. \]

The same result is obtained when we use K = 54eV in Equation \ref{6.61}. The proximity of this theoretical result to the Davisson–Germer experimental value of λ = 1.64 Å is a convincing argument for the existence of de Broglie matter waves.

$Figure shows the surface diffraction of a monochromatic electromagnetic wave on a crystalline lattice structure. The in-phase incident beams are reflected from atoms on the surface. Phi is the angle between the incident and the reflected beam, the in-plane distance between the atoms is a.$

Diffraction lines measured with low-energy electrons, such as those used in the Davisson–Germer experiment, are quite broad (Figure $\PageIndex{3}$) because the incident electrons are scattered only from the surface. The resolution of diffraction images greatly improves when a higher-energy electron beam passes through a thin metal foil. This occurs because the diffraction image is created by scattering off many crystalline planes inside the volume, and the maxima produced in scattering at Bragg angles are sharp (Figure $\PageIndex{5}$).

$Picture A is a photograph of the diffraction pattern obtained in scattering on a crystalline solid with X-rays. Picture B is a photograph of the diffraction pattern obtained in scattering on a crystalline solid with electrons. Both pictures demonstrate diffracted spots symmetrically arranged around the central beam.$

Since the work of Davisson and Germer, de Broglie’s hypothesis has been extensively tested with various experimental techniques, and the existence of de Broglie waves has been confirmed for numerous elementary particles. Neutrons have been used in scattering experiments to determine crystalline structures of solids from interference patterns formed by neutron matter waves. The neutron has zero charge and its mass is comparable with the mass of a positively charged proton. Both neutrons and protons can be seen as matter waves. Therefore, the property of being a matter wave is not specific to electrically charged particles but is true of all particles in motion. Matter waves of molecules as large as carbon $C_{60}$ have been measured. All physical objects, small or large, have an associated matter wave as long as they remain in motion. The universal character of de Broglie matter waves is firmly established.

Example $\PageIndex{3A}$: Neutron Scattering

Suppose that a neutron beam is used in a diffraction experiment on a typical crystalline solid. Estimate the kinetic energy of a neutron (in eV) in the neutron beam and compare it with kinetic energy of an ideal gas in equilibrium at room temperature.

We assume that a typical crystal spacing a is of the order of 1.0 Å. To observe a diffraction pattern on such a lattice, the neutron wavelength λ must be on the same order of magnitude as the lattice spacing. We use Equation \ref{6.61} to find the momentum p and kinetic energy K . To compare this energy with the energy $E_T$ of ideal gas in equilibrium at room temperature $T = 300 \, K$, we use the relation $K = 3/2 k_BT$, where $k_B = 8.62 \times 10^{-5}eV/K$ is the Boltzmann constant.

We evaluate pc to compare it with the neutron’s rest mass energy $E_0 = 940 \, MeV$:

\[p = \frac{h}{\lambda} \Rightarrow pc = \frac{hc}{\lambda} = \frac{1.241 \times 10^{-6}eV \cdot m}{10^{-10}m} = 12.41 \, keV. \nonumber \]

We see that $p^2c^2 << E_0^2$ and we can use the nonrelativistic kinetic energy:

\[K = \frac{p^2}{2m_n} = \frac{h^2}{2\lambda^2 m_n} = \frac{(6.63\times 10^{−34}J \cdot s)^2}{(2\times 10^{−20}m^2)(1.66 \times 10^{−27} kg)} = 1.32 \times 10^{−20} J = 82.7 \, meV. \nonumber \]

Kinetic energy of ideal gas in equilibrium at 300 K is:

\[K_T = \frac{3}{2}k_BT = \frac{3}{2} (8.62 \times 10^{-5}eV/K)(300 \, K) = 38.8 \, MeV. \nonumber \]

We see that these energies are of the same order of magnitude.

Neutrons with energies in this range, which is typical for an ideal gas at room temperature, are called “thermal neutrons.”

Example $\PageIndex{3B}$: Wavelength of a Relativistic Proton

In a supercollider at CERN, protons can be accelerated to velocities of 0.75 c . What are their de Broglie wavelengths at this speed? What are their kinetic energies?

The rest mass energy of a proton is $E_0 = m_0c^2 = (1.672 \times 10^{−27} kg)(2.998 \times 10^8m/s)^2 = 938 \, MeV$. When the proton’s velocity is known, we have β = 0.75 and $\beta \gamma = 0.75 / \sqrt{1 - 0.75^2} = 1.714$. We obtain the wavelength λλ and kinetic energy K from relativistic relations.

\[\lambda = \frac{h}{p} = \frac{hc}{\beta \gamma E_0} = \frac{1.241 \, eV \cdot \mu m}{1.714 (938 \, MeV)} = 0.77 \, fm \nonumber \]

\[K = E_0(\gamma - 1) = 938 \, MeV (1 /\sqrt{1 - 0.75^2} - 1) = 480.1\, MeV \nonumber \]

Notice that because a proton is 1835 times more massive than an electron, if this experiment were performed with electrons, a simple rescaling of these results would give us the electron’s wavelength of (1835)0.77 fm = 1.4 pm and its kinetic energy of 480.1 MeV /1835 = 261.6 keV.

Exercise $\PageIndex{3}$

Find the de Broglie wavelength and kinetic energy of a free electron that travels at a speed of 0.75 c .

$\lambda = 1.417 \, pm; \, K = 261.56 \, keV$

6.5 De Broglie’s Matter Waves

Learning objectives.

By the end of this section, you will be able to:

Describe de Broglie’s hypothesis of matter waves
Explain how the de Broglie’s hypothesis gives the rationale for the quantization of angular momentum in Bohr’s quantum theory of the hydrogen atom
Describe the Davisson–Germer experiment
Interpret de Broglie’s idea of matter waves and how they account for electron diffraction phenomena

According to de Broglie’s hypothesis, massless photons as well as massive particles must satisfy one common set of relations that connect the energy E with the frequency f , and the linear momentum p with the wavelength λ . λ . We have discussed these relations for photons in the context of Compton’s effect. We are recalling them now in a more general context. Any particle that has energy and momentum is a de Broglie wave of frequency f and wavelength λ : λ :

Here, E and p are, respectively, the relativistic energy and the momentum of a particle. De Broglie’s relations are usually expressed in terms of the wave vector k → , k → , k = 2 π / λ , k = 2 π / λ , and the wave frequency ω = 2 π f , ω = 2 π f , as we usually do for waves:

Wave theory tells us that a wave carries its energy with the group velocity . For matter waves, this group velocity is the velocity u of the particle. Identifying the energy E and momentum p of a particle with its relativistic energy m c 2 m c 2 and its relativistic momentum mu , respectively, it follows from de Broglie relations that matter waves satisfy the following relation:

where β = u / c . β = u / c . When a particle is massless we have u = c u = c and Equation 6.57 becomes λ f = c . λ f = c .

Example 6.11

How long are de broglie matter waves.

Depending on the problem at hand, in this equation we can use the following values for hc : h c = ( 6.626 × 10 −34 J · s ) ( 2.998 × 10 8 m/s ) = 1.986 × 10 −25 J · m = 1.241 eV · μ m h c = ( 6.626 × 10 −34 J · s ) ( 2.998 × 10 8 m/s ) = 1.986 × 10 −25 J · m = 1.241 eV · μ m

For the basketball, the kinetic energy is K = m u 2 / 2 = ( 0.65 kg ) ( 10 m/s ) 2 / 2 = 32.5 J K = m u 2 / 2 = ( 0.65 kg ) ( 10 m/s ) 2 / 2 = 32.5 J and the rest mass energy is E 0 = m c 2 = ( 0.65 kg ) ( 2.998 × 10 8 m/s ) 2 = 5.84 × 10 16 J. E 0 = m c 2 = ( 0.65 kg ) ( 2.998 × 10 8 m/s ) 2 = 5.84 × 10 16 J. We see that K / ( K + E 0 ) ≪ 1 K / ( K + E 0 ) ≪ 1 and use p = m u = ( 0.65 kg ) ( 10 m/s ) = 6.5 J · s/m : p = m u = ( 0.65 kg ) ( 10 m/s ) = 6.5 J · s/m : λ = h p = 6.626 × 10 −34 J · s 6.5 J · s/m = 1.02 × 10 −34 m . λ = h p = 6.626 × 10 −34 J · s 6.5 J · s/m = 1.02 × 10 −34 m .
For the nonrelativistic electron, E 0 = m c 2 = ( 9.109 × 10 −31 kg ) ( 2.998 × 10 8 m/s ) 2 = 511 keV E 0 = m c 2 = ( 9.109 × 10 −31 kg ) ( 2.998 × 10 8 m/s ) 2 = 511 keV and when K = 1.0 eV , K = 1.0 eV , we have K / ( K + E 0 ) = ( 1 / 512 ) × 10 −3 ≪ 1 , K / ( K + E 0 ) = ( 1 / 512 ) × 10 −3 ≪ 1 , so we can use the nonrelativistic formula. However, it is simpler here to use Equation 6.58 : λ = h p = h c K ( K + 2 E 0 ) = 1.241 eV · μ m ( 1.0 eV ) [ 1.0 eV+ 2 ( 511 keV ) ] = 1.23 nm . λ = h p = h c K ( K + 2 E 0 ) = 1.241 eV · μ m ( 1.0 eV ) [ 1.0 eV+ 2 ( 511 keV ) ] = 1.23 nm . If we use nonrelativistic momentum, we obtain the same result because 1 eV is much smaller than the rest mass of the electron.
For a fast electron with K = 108 keV, K = 108 keV, relativistic effects cannot be neglected because its total energy is E = K + E 0 = 108 keV + 511 keV = 619 keV E = K + E 0 = 108 keV + 511 keV = 619 keV and K / E = 108 / 619 K / E = 108 / 619 is not negligible: λ = h p = h c K ( K + 2 E 0 ) = 1.241 eV · μm 108 keV [ 108 keV + 2 ( 511 keV ) ] = 3.55 pm . λ = h p = h c K ( K + 2 E 0 ) = 1.241 eV · μm 108 keV [ 108 keV + 2 ( 511 keV ) ] = 3.55 pm .

Significance

Check your understanding 6.11.

What is de Broglie’s wavelength of a nonrelativistic proton with a kinetic energy of 1.0 eV?

Using the concept of the electron matter wave, de Broglie provided a rationale for the quantization of the electron’s angular momentum in the hydrogen atom, which was postulated in Bohr’s quantum theory. The physical explanation for the first Bohr quantization condition comes naturally when we assume that an electron in a hydrogen atom behaves not like a particle but like a wave. To see it clearly, imagine a stretched guitar string that is clamped at both ends and vibrates in one of its normal modes. If the length of the string is l ( Figure 6.18 ), the wavelengths of these vibrations cannot be arbitrary but must be such that an integer k number of half-wavelengths λ / 2 λ / 2 fit exactly on the distance l between the ends. This is the condition l = k λ / 2 l = k λ / 2 for a standing wave on a string. Now suppose that instead of having the string clamped at the walls, we bend its length into a circle and fasten its ends to each other. This produces a circular string that vibrates in normal modes, satisfying the same standing-wave condition, but the number of half-wavelengths must now be an even number k , k = 2 n , k , k = 2 n , and the length l is now connected to the radius r n r n of the circle. This means that the radii are not arbitrary but must satisfy the following standing-wave condition:

If an electron in the n th Bohr orbit moves as a wave, by Equation 6.59 its wavelength must be equal to λ = 2 π r n / n . λ = 2 π r n / n . Assuming that Equation 6.58 is valid, the electron wave of this wavelength corresponds to the electron’s linear momentum, p = h / λ = n h / ( 2 π r n ) = n ℏ / r n . p = h / λ = n h / ( 2 π r n ) = n ℏ / r n . In a circular orbit, therefore, the electron’s angular momentum must be

This equation is the first of Bohr’s quantization conditions, given by Equation 6.36 . Providing a physical explanation for Bohr’s quantization condition is a convincing theoretical argument for the existence of matter waves.

Example 6.12

The electron wave in the ground state of hydrogen, check your understanding 6.12.

Find the de Broglie wavelength of an electron in the third excited state of hydrogen.

In the particular experiment that provided the very first evidence of electron waves (known today as the Davisson–Germer experiment ), they studied a surface of nickel. Their nickel sample was specially prepared in a high-temperature oven to change its usual polycrystalline structure to a form in which large single-crystal domains occupy the volume. Figure 6.19 shows the experimental setup. Thermal electrons are released from a heated element (usually made of tungsten) in the electron gun and accelerated through a potential difference Δ V , Δ V , becoming a well-collimated beam of electrons produced by an electron gun. The kinetic energy K of the electrons is adjusted by selecting a value of the potential difference in the electron gun. This produces a beam of electrons with a set value of linear momentum, in accordance with the conservation of energy:

The electron beam is incident on the nickel sample in the direction normal to its surface. At the surface, it scatters in various directions. The intensity of the beam scattered in a selected direction φ φ is measured by a highly sensitive detector. The detector’s angular position with respect to the direction of the incident beam can be varied from φ = 0 ° φ = 0 ° to φ = 90 ° . φ = 90 ° . The entire setup is enclosed in a vacuum chamber to prevent electron collisions with air molecules, as such thermal collisions would change the electrons’ kinetic energy and are not desirable.

When the nickel target has a polycrystalline form with many randomly oriented microscopic crystals, the incident electrons scatter off its surface in various random directions. As a result, the intensity of the scattered electron beam is much the same in any direction, resembling a diffuse reflection of light from a porous surface. However, when the nickel target has a regular crystalline structure, the intensity of the scattered electron beam shows a clear maximum at a specific angle and the results show a clear diffraction pattern (see Figure 6.20 ). Similar diffraction patterns formed by X-rays scattered by various crystalline solids were studied in 1912 by father-and-son physicists William H. Bragg and William L. Bragg . The Bragg law in X-ray crystallography provides a connection between the wavelength λ λ of the radiation incident on a crystalline lattice, the lattice spacing, and the position of the interference maximum in the diffracted radiation (see Diffraction ).

The lattice spacing of the Davisson–Germer target, determined with X-ray crystallography, was measured to be a = 2.15 Å . a = 2.15 Å . Unlike X-ray crystallography in which X-rays penetrate the sample, in the original Davisson–Germer experiment, only the surface atoms interact with the incident electron beam. For the surface diffraction, the maximum intensity of the reflected electron beam is observed for scattering angles that satisfy the condition n λ = a sin φ n λ = a sin φ (see Figure 6.21 ). The first-order maximum (for n = 1 n = 1 ) is measured at a scattering angle of φ ≈ 50 ° φ ≈ 50 ° at Δ V ≈ 54 V , Δ V ≈ 54 V , which gives the wavelength of the incident radiation as λ = ( 2.15 Å ) sin 50 ° = 1.64 Å . λ = ( 2.15 Å ) sin 50 ° = 1.64 Å . On the other hand, a 54-V potential accelerates the incident electrons to kinetic energies of K = 54 eV . K = 54 eV . Their momentum, calculated from Equation 6.61 , is p = 2.478 × 10 −5 eV · s / m . p = 2.478 × 10 −5 eV · s / m . When we substitute this result in Equation 6.58 , the de Broglie wavelength is obtained as

The same result is obtained when we use K = 54 eV K = 54 eV in Equation 6.61 . The proximity of this theoretical result to the Davisson–Germer experimental value of λ = 1.64 Å λ = 1.64 Å is a convincing argument for the existence of de Broglie matter waves.

Diffraction lines measured with low-energy electrons, such as those used in the Davisson–Germer experiment, are quite broad (see Figure 6.20 ) because the incident electrons are scattered only from the surface. The resolution of diffraction images greatly improves when a higher-energy electron beam passes through a thin metal foil. This occurs because the diffraction image is created by scattering off many crystalline planes inside the volume, and the maxima produced in scattering at Bragg angles are sharp (see Figure 6.22 ).

Since the work of Davisson and Germer, de Broglie’s hypothesis has been extensively tested with various experimental techniques, and the existence of de Broglie waves has been confirmed for numerous elementary particles. Neutrons have been used in scattering experiments to determine crystalline structures of solids from interference patterns formed by neutron matter waves. The neutron has zero charge and its mass is comparable with the mass of a positively charged proton. Both neutrons and protons can be seen as matter waves. Therefore, the property of being a matter wave is not specific to electrically charged particles but is true of all particles in motion. Matter waves of molecules as large as carbon C 60 C 60 have been measured. All physical objects, small or large, have an associated matter wave as long as they remain in motion. The universal character of de Broglie matter waves is firmly established.

Example 6.13

Neutron scattering.

We see that p 2 c 2 ≪ E 0 2 p 2 c 2 ≪ E 0 2 so K ≪ E 0 K ≪ E 0 and we can use the nonrelativistic kinetic energy:

Kinetic energy of ideal gas in equilibrium at 300 K is:

We see that these energies are of the same order of magnitude.

Example 6.14

Wavelength of a relativistic proton, check your understanding 6.13.

Find the de Broglie wavelength and kinetic energy of a free electron that travels at a speed of 0.75 c .

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-3/pages/1-introduction

Authors: Samuel J. Ling, Jeff Sanny, William Moebs
Publisher/website: OpenStax
Book title: University Physics Volume 3
Publication date: Sep 29, 2016
Location: Houston, Texas
Book URL: https://openstax.org/books/university-physics-volume-3/pages/1-introduction
Section URL: https://openstax.org/books/university-physics-volume-3/pages/6-5-de-broglies-matter-waves

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Reset password New user? Sign up

Existing user? Log in

De Broglie Hypothesis

Already have an account? Log in here.

Today we know that every particle exhibits both matter and wave nature. This is called wave-particle duality . The concept that matter behaves like wave is called the de Broglie hypothesis , named after Louis de Broglie, who proposed it in 1924.

De Broglie Equation

Explanation of bohr's quantization rule.

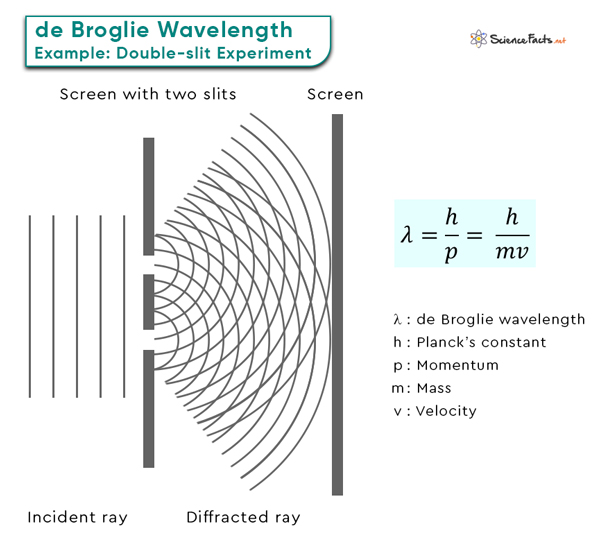
De Broglie gave the following equation which can be used to calculate de Broglie wavelength, $\lambda$, of any massed particle whose momentum is known:

\[\lambda = \frac{h}{p},\]

where $h$ is the Plank's constant and $p$ is the momentum of the particle whose wavelength we need to find.

With some modifications the following equation can also be written for velocity $(v)$ or kinetic energy $(K)$ of the particle (of mass $m$):

\[\lambda = \frac{h}{mv} = \frac{h}{\sqrt{2mK}}.\]

Notice that for heavy particles, the de Broglie wavelength is very small, in fact negligible. Hence, we can conclude that though heavy particles do exhibit wave nature, it can be neglected as it's insignificant in all practical terms of use.

Calculate the de Broglie wavelength of a golf ball whose mass is 40 grams and whose velocity is 6 m/s. We have \[\lambda = \frac{h}{mv} = \frac{6.63 \times 10^{-34}}{40 \times 10^{-3} \times 6} \text{ m}=2.76 \times 10^{-33} \text{ m}.\ _\square\]

One of the main limitations of Bohr's atomic theory was that no justification was given for the principle of quantization of angular momentum. It does not explain the assumption that why an electron can rotate only in those orbits in which the angular momentum of the electron, $mvr,$ is a whole number multiple of $ \frac{h}{2\pi} $.

De Broglie successfully provided the explanation to Bohr's assumption by his hypothesis.

Problem Loading...

Note Loading...

Set Loading...

De Broglie Hypothesis

The De Broglie Hypothesis is a fundamental concept in proposed by the French physicist Louis de Broglie in 1924. This groundbreaking idea introduced the wave-particle duality of matter, suggesting that not only light (previously understood to exhibit both wave-like and particle-like properties) but all forms of matter have wave-like characteristics.

De Broglie Equation Derivation

Louis de Broglie hypothesized that if light can display dual characteristics (both wave-like and particle-like properties), then particles, such as electrons, might also exhibit similar dual characteristics. His derivation was based on the parallels between the equations for energy and momentum in both light and material particles.

Step 1: Relating Energy and Momentum for Light

For photons (light particles), the energy (𝐸 E ) and momentum (𝑝 p ) are related by the equations:

Here, ℎ h is Planck’s constant, 𝑓 f is the frequency of the photon, and 𝑐 c is the speed of light. By substituting the energy equation into the momentum equation, we get:

Since the wavelength ( λ ) of a photon is related to its frequency by 𝑐 = 𝜆𝑓, we can rewrite 𝑓 as:

Substituting back, the momentum of a photon can be expressed as:

Step 2: Applying the Concept to Material Particles

De Broglie proposed that if light (which was known to have wave-like properties) has a wavelength given 𝜆 = ℎ/𝑝, then particles, such as electrons, should also have a wavelength describable by a similar relationship, even though they have mass. Thus, he extended the equation to all matter, proposing that:

where p is now the momentum of the particle, which for a non-relativistic particle is given by:

Here, m is the mass of the particle and v is its velocity.

Step 3: De Broglie Wavelength of Particles

Combining the expressions, the de Broglie wavelength for any particle is thus given by:

This equation implies that every moving particle has a wave associated with it, and the wavelength of that wave is inversely proportional to the particle’s momentum. This groundbreaking idea led to the development of wave mechanics and has been fundamental in many areas of quantum physics, such as the theory behind quantum fields and elementary particles.

De Broglie Wavelength for an Electron

To calculate the De Broglie wavelength of an electron, we use the formula derived by Louis de Broglie which relates a particle’s wavelength to its momentum. The formula is:

𝜆 is the wavelength,
ℎ is Planck’s constant, approximately 6.626×10⁻³⁴ Joule seconds,
𝑝 is the momentum of the electron.

Calculating Momentum

The momentum 𝑝 p of an electron can be calculated using the formula: 𝑝=𝑚𝑣 p = m v where:

𝑚 is the mass of the electron, approximately 9.109×10⁻³¹ kg,
𝑣 is the velocity of the electron.

Significance of the De Broglie Equation

The De Broglie equation , 𝜆 = ℎ/𝑝 , is a cornerstone in quantum mechanics, providing a profound understanding of the wave-particle duality of matter. Its implications extend far beyond theoretical physics, impacting various scientific fields and technologies.

Fundamental to Quantum Mechanics

The equation integrates wave-like behavior into the description of elementary particles, bridging a gap between classical and quantum physics. This wave-particle duality is essential for the development of quantum mechanics, influencing the theoretical framework that describes how subatomic particles behave.

Basis for Modern Physics Theories

De Broglie’s insights laid the groundwork for Schrödinger to formulate his wave equation, which uses the concept of wavefunctions to describe the statistical behavior of systems. The wave-particle duality concept is integral to quantum field theory, which extends quantum mechanics to more complex systems including fields and forces.

Experimental Validation and Applications

The equation has been empirically validated through experiments such as electron diffraction and neutron diffraction, which demonstrate that particles exhibit wave-like behavior under certain conditions. These experiments are pivotal for technologies such as electron microscopes, which rely on electron waves to achieve high-resolution imaging beyond the capability of traditional optical microscopes.

Technological Impact

Understanding the wave properties of particles enables the exploitation of phenomena such as quantum tunneling, utilized in devices like tunnel diodes and the scanning tunneling microscope. These applications are crucial in electronics and materials science, where quantum effects are significant.

Educational and Conceptual Influence

The De Broglie equation has also profoundly impacted educational approaches in physics, providing a fundamental concept that challenges and expands our understanding of the natural world. It encourages a more nuanced view of matter, essential for students and researchers delving into quantum physics.

Relation between De Broglie Equation and Bohr’s Hypothesis of Atom

De broglie’s equation.

Louis de Broglie introduced his theory of electron waves in 1924, which proposed that particles could exhibit properties of waves. His famous equation relates the wavelength of a particle to its momentum: 𝜆 = ℎ/𝑝 where 𝜆is the wavelength, ℎ is Planck’s constant, and 𝑝 p is the momentum of the particle.

Bohr’s Hypothesis of the Atom

Niels Bohr proposed his model of the atom in 1913. His key hypothesis was that electrons orbit the nucleus in distinct orbits without radiating energy, contrary to what classical electromagnetism would predict. To explain the stability of these orbits, Bohr introduced the concept of quantization:

Electrons can only occupy certain allowed orbits.
The angular momentum of electrons in these orbits is quantized, specifically, it is an integer multiple of the reduced Planck constant
(ℏ): 𝐿 = 𝑛×ℎ/2𝜋 = 𝑛ℏ
where 𝐿 L is the angular momentum, n is a positive integer (quantum number), and h is Planck’s constant.

Integrating De Broglie’s Equation with Bohr’s Model

De Broglie’s theory was revolutionary because it provided a theoretical justification for Bohr’s quantization condition by interpreting the electron not just as a particle, but as a wave that must form a standing wave pattern around the nucleus. For the electron wave to be stable and not interfere destructively with itself, the circumference of the electron’s orbit must be an integer multiple of its wavelength:

where 𝑟 is the radius of the electron’s orbit, and n is an integer. This condition ensures that the wave ‘fits’ perfectly into its orbital path around the nucleus.

Substituting De Broglie’s Equation

By substituting De Broglie’s expression for the wavelength into the condition for a stable orbit, we get:

Using the expression for momentum 𝑝=𝑚𝑣 p = mv and the definition of angular momentum 𝐿=𝑚𝑣𝑟 L = mvr , we can relate this to Bohr’s quantization of angular momentum:

Thus, De Broglie’s hypothesis not only supported Bohr’s model but also suggested a deeper wave nature of the electron. It bridged the gap between the quantized orbits of Bohr’s atom model and the wave-like behavior of particles, paving the way for modern quantum mechanics, which would further refine and expand these ideas in the Schrodinger equation and beyond.

Examples of De Broglie Hypothesis

Electron Diffraction

One of the first confirmations of De Broglie’s hypothesis was the observation of electron diffraction patterns. When electrons are passed through thin metal foils or across a crystal, they produce diffraction patterns similar to those produced by light waves, confirming that electrons behave as waves under certain conditions.

Scanning Tunneling Microscope (STM)

The scanning tunneling microscope, which can image surfaces at the atomic level, operates based on the quantum tunneling of electrons between the microscope’s tip and the surface. The wave nature of electrons, as predicted by De Broglie, is fundamental to the operation of this instrument.

Bohr Model of the Atom

De Broglie’s ideas extended the Bohr model by providing a theoretical basis for the quantization of electron orbits in atoms. His hypothesis suggested that electrons form standing wave patterns around the nucleus, which only occur at certain discrete (quantized) orbits.

Matter Waves

The concept of matter waves is essential in fields like quantum mechanics and has led to further developments in wave mechanics. This includes the use of neutrons, atoms, and molecules in wave-like applications, similar to how light and electrons are used.

Neutron Interferometry

Neutron beams, used in neutron interferometry, exhibit wave-like interference effects. These experiments have provided precise measurements of neutron properties and fundamental quantum phenomena, supporting De Broglie’s hypothesis at larger scales.

Atomic Force Microscopy (AFM)

AFM, like STM, uses the principles of quantum mechanics and the wave-like properties of atoms on a surface to achieve high-resolution imaging. The forces between the tip’s atoms and the sample’s atoms are influenced by their wave functions.

How was the De Broglie Equation derived?

Louis de Broglie proposed that particles of matter, like electrons, could exhibit wave-like properties similar to light. Combining Einstein’s equation relating energy and mass (𝐸 = 𝑚𝑐²) with Planck’s equation relating energy and frequency (𝐸 = ℎ𝑓), and considering the wave equation (𝑐 = 𝑓𝜆), De Broglie derived his hypothesis that matter behaves as waves.

Why is the De Broglie Equation important?

The De Broglie Equation is crucial for understanding quantum mechanics as it introduces the concept of wave-particle duality. This concept states that every particle or quantum entity can exhibit both particle-like and wave-like behavior. It forms the basis for the development of quantum theory, particularly in the formulation of wave mechanics.

Can the De Broglie Equation be applied to all objects?

While theoretically applicable to all matter, in practice, the wave-like properties described by the De Broglie Equation are significant only for very small objects, like subatomic particles. For larger objects, the wavelengths calculated by the equation become so small that they are not detectable with current technology.

What is wave-particle duality?

Wave-particle duality is a fundamental concept of quantum mechanics that suggests that every particle or quantum entity may be partly described in terms not only of particles, but also of waves. It means that elementary particles such as electrons and photons exhibit both particle-like and wave-like properties, depending on the experimental setup.

AI Generator

Text prompt

Instructive
Professional

10 Examples of Public speaking

20 Examples of Gas lighting

De Broglie Hypothesis

Does All Matter Exhibit Wave-like Properties?

Quantum Physics
Physics Laws, Concepts, and Principles
Important Physicists
Thermodynamics
Cosmology & Astrophysics
Weather & Climate

M.S., Mathematics Education, Indiana University
B.A., Physics, Wabash College

The De Broglie hypothesis proposes that all matter exhibits wave-like properties and relates the observed wavelength of matter to its momentum. After Albert Einstein's photon theory became accepted, the question became whether this was true only for light or whether material objects also exhibited wave-like behavior. Here is how the De Broglie hypothesis was developed.

De Broglie's Thesis

In his 1923 (or 1924, depending on the source) doctoral dissertation, the French physicist Louis de Broglie made a bold assertion. Considering Einstein's relationship of wavelength lambda to momentum p , de Broglie proposed that this relationship would determine the wavelength of any matter, in the relationship:

lambda = h / p

recall that h is Planck's constant

This wavelength is called the de Broglie wavelength . The reason he chose the momentum equation over the energy equation is that it was unclear, with matter, whether E should be total energy, kinetic energy, or total relativistic energy. For photons, they are all the same, but not so for matter.

Assuming the momentum relationship, however, allowed the derivation of a similar de Broglie relationship for frequency f using the kinetic energy E k :

f = E k / h

Alternate Formulations

De Broglie's relationships are sometimes expressed in terms of Dirac's constant, h-bar = h / (2 pi ), and the angular frequency w and wavenumber k :

p = h-bar * kE k

= h-bar * w

Experimental Confirmation

In 1927, physicists Clinton Davisson and Lester Germer, of Bell Labs, performed an experiment where they fired electrons at a crystalline nickel target. The resulting diffraction pattern matched the predictions of the de Broglie wavelength. De Broglie received the 1929 Nobel Prize for his theory (the first time it was ever awarded for a Ph.D. thesis) and Davisson/Germer jointly won it in 1937 for the experimental discovery of electron diffraction (and thus the proving of de Broglie's hypothesis).

Further experiments have held de Broglie's hypothesis to be true, including the quantum variants of the double slit experiment . Diffraction experiments in 1999 confirmed the de Broglie wavelength for the behavior of molecules as large as buckyballs, which are complex molecules made up of 60 or more carbon atoms.

Significance of the de Broglie Hypothesis

The de Broglie hypothesis showed that wave-particle duality was not merely an aberrant behavior of light, but rather was a fundamental principle exhibited by both radiation and matter. As such, it becomes possible to use wave equations to describe material behavior, so long as one properly applies the de Broglie wavelength. This would prove crucial to the development of quantum mechanics. It is now an integral part of the theory of atomic structure and particle physics.

Macroscopic Objects and Wavelength

Though de Broglie's hypothesis predicts wavelengths for matter of any size, there are realistic limits on when it's useful. A baseball thrown at a pitcher has a de Broglie wavelength that is smaller than the diameter of a proton by about 20 orders of magnitude. The wave aspects of a macroscopic object are so tiny as to be unobservable in any useful sense, although interesting to muse about.

Wave Particle Duality and How It Works
de Broglie Equation Definition
De Broglie Wavelength Example Problem
Wave-Particle Duality - Definition
Quantum Physics Overview
Top 10 Weird but Cool Physics Ideas
The Photoelectric Effect
What the Compton Effect Is and How It Works in Physics
Understanding the Heisenberg Uncertainty Principle
Photoelectric Effect: Electrons from Matter and Light
Erwin Schrödinger and the Schrödinger's Cat Thought Experiment
What Is a Photon in Physics?
Orbital Definition and Example
How to Solve an Energy From Wavelength Problem
A Brief History of Atomic Theory
Photon Definition

What is De Broglie Hypothesis?

De broglie's hypothesis says that matter consists of both the particle nature as well as wave nature. de broglie wavelength λ is given as λ = h p , where p represents the particle momentum and can be written as: λ = h m v where, h is the planck's constant, m is the mass of the particle, and v is the velocity of the particle. from the above relation, it can be said that the wavelength of the matter is inversely proportional to the magnitude of the particle's linear momentum. this relation is applicable to both microscopic and macroscopic particles the de broglie equation is one of the equations that is commonly used to define the wave properties of matter. electromagnetic radiation exhibits the dual nature of a particle (having a momentum) and wave (expressed in frequency, and wavelength)..

Talk to our experts

1800-120-456-456

De Broglie Equation

Introduction

The wave nature of light was the only aspect that was considered until Neil Bohr’s model. Later, however, Max Planck in his explanation of quantum theory hypothesized that light is made of very minute pockets of energy which are in turn made of photons or quanta. It was then considered that light has a particle nature and every packet of light always emits a certain fixed amount of energy.

By this, the energy of photons can be expressed as:

E = hf = h * c/λ

Here, h is Plank’s constant

F refers to the frequency of the waves

Λ implies the wavelength of the pockets

Therefore, this basically insinuates that light has both the properties of particle duality as well as wave.

Louis de Broglie was a student of Bohr, who then formulated his own hypothesis of wave-particle duality, drawn from this understanding of light. Later on, when this hypothesis was proven true, it became a very important concept in particle physics.

⇒ Don't Miss Out: Get Your Free JEE Main Rank Predictor 2024 Instantly! 🚀

What is the De Broglie Equation?

Quantum mechanics assumes matter to be both like a wave as well as a particle at the sub-atomic level. The De Broglie equation states that every particle that moves can sometimes act as a wave, and sometimes as a particle. The wave which is associated with the particles that are moving are known as the matter-wave, and also as the De Broglie wave. The wavelength is known as the de Broglie wavelength.

For an electron, de Broglie wavelength equation is:

λ = \[\frac{h}{mv}\]

Here, λ points to the wave of the electron in question

M is the mass of the electron

V is the velocity of the electron

Mv is the momentum that is formed as a result

It was found out that this equation works and applies to every form of matter in the universe, i.e, Everything in this universe, from living beings to inanimate objects, all have wave particle duality.

Significance of De Broglie Equation

De Broglie says that all the objects that are in motion have a particle nature. However, if we look at a moving ball or a moving car, they don’t seem to have particle nature. To make this clear, De Broglie derived the wavelengths of electrons and a cricket ball. Now, let’s understand how he did this.

De Broglie Wavelength

1. De Broglie Wavelength for a Cricket Ball

Let’s say,Mass of the ball = 150 g (150 x 10⁻³ kg),

Velocity = 35 m/s,

and h = 6.626 x 10⁻³⁴ Js

Now, putting these values in the equation

λ = (6.626 * 10 to power of -34)/ (150 * 10 to power of -3 *35)

This yields

λBALL = 1.2621 x 10 to the power of -34 m,

Which is 1.2621 x 10 to the power of -24 Å.

We know that Å is a very small unit, and therefore the value is in the power of 10−24−24^{-24}, which is a very small value. From here, we see that the moving cricket ball is a particle.

Now, the question arises if this ball has a wave nature or not. Your answer will be a big no because the value of λBALL is immeasurable. This proves that de Broglie’s theory of wave-particle duality is valid for the moving objects ‘up to’ the size (not equal to the size) of the electrons.

De Broglie Wavelength for an Electron

We know that me = 9.1 x 10 to power of -31 kg

and ve = 218 x 10 to power of -6 m/s

Now, putting these values in the equation λ = h/mv, which yields λ = 3.2 Å.

This value is measurable. Therefore, we can say that electrons have wave-particle duality. Thus all the big objects have a wave nature and microscopic objects like electrons have wave-particle nature.

E = hν = \[\frac{hc}{\lambda }\]

The Conclusion of De Broglie Hypothesis

From de Broglie equation for a material particle, i.e.,

λ = \[\frac{h}{p}\]or \[\frac{h}{mv}\], we conclude the following:

i. If v = 0, then λ = ∞, and

If v = ∞, then λ = 0

It means that waves are associated with the moving material particles only. This implies these waves are independent of their charge.

FAQs on De Broglie Equation

1.The De Broglie hypothesis was confirmed through which means?

De Broglie had not proved the validity of his hypothesis on his own, it was merely a hypothetical assumption before it was tested out and consequently, it was found that all substances in the universe have wave-particle duality. A number of experiments were conducted with Fresnel diffraction as well as a specular reflection of neutral atoms. These experiments proved the validity of De Broglie’s statements and made his hypothesis come true. These experiments were conducted by some of his students.

2.What exactly does the De Broglie equation apply to?

In very broad terms, this applies to pretty much everything in the tangible universe. This means that people, non-living things, trees and animals, all of these come under the purview of the hypothesis. Any particle of any substance that has matter and has linear momentum also is a wave. The wavelength will be inversely related to the magnitude of the linear momentum of the particle. Therefore, everything in the universe that has matter, is applicable to fit under the De Broglie equation.

3.Is it possible that a single photon also has a wavelength?

When De Broglie had proposed his hypothesis, he derived from the work of Planck that light is made up of small pockets that have a certain energy, known as photons. For his own hypothesis, he said that all things in the universe that have to matter have wave-particle duality, and therefore, wavelength. This extends to light as well, since it was proved that light is made up of matter (photons). Hence, it is true that even a single photon has a wavelength.

4.Are there any practical applications of the De Broglie equation?

It would be wrong to say that people use this equation in their everyday lives, because they do not, not in the literal sense at least. However, practical applications do not only refer to whether they can tangibly be used by everyone. The truth of the De Broglie equation lies in the fact that we, as human beings, also are made of matter and thus we also have wave-particle duality. All the things we work with have wave-particle duality.

5.Does the De Broglie equation apply to an electron?

Yes, this equation is applicable for every single moving body in the universe, down to the smallest subatomic levels. Just how light particles like photons have their own wavelengths, it is also true for an electron. The equation treats electrons as both waves as well as particles, only then will it have wave-particle duality. For every electron of every atom of every element, this stands true and using the equation mentioned, the wavelength of an electron can also be calculated.

6.Derive the relation between De Broglie wavelength and temperature.

We know that the average KE of a particle is:

K = 3/2 k b T

Where k b is Boltzmann’s constant, and

T = temperature in Kelvin

The kinetic energy of a particle is ½ mv²

The momentum of a particle, p = mv = √2mK

= √2m(3/2)KbT = √2mKbT

de Broglie wavelength, λ = h/p = h√2mkbT

7.If an electron behaves like a wave, what should determine its wavelength and frequency?

Momentum and energy determine the wavelength and frequency of an electron.

8. Find λ associated with an H 2 of mass 3 a.m.u moving with a velocity of 4 km/s.

Here, v = 4 x 10³ m/s

Mass of hydrogen = 3 a.m.u = 3 x 1.67 x 10⁻²⁷kg = 5 x 10⁻²⁷kg

On putting these values in the equation λ = h/mv we get

λ = (6.626 x 10⁻³⁴)/(4 x 10³ x 5 x 10⁻²⁷) = 3 x 10⁻¹¹ m.

9. If the KE of an electron increases by 21%, find the percentage change in its De Broglie wavelength.

We know that λ = h/√2mK

So, λ i = h/√(2m x 100) , and λ f = h/√(2m x 121)

% change in λ is:

Change in wavelength/Original x 100 = (λ fi - λ f )/λ i = ((h/√2m)(1/10 - 1/21))/(h/√2m)(1/10)

On solving, we get

% change in λ = 5.238 %

Photons and Matter Waves

De Broglie’s Matter Waves

Samuel J. Ling; Jeff Sanny; and William Moebs

Learning Objectives

By the end of this section, you will be able to:

Describe de Broglie’s hypothesis of matter waves
Explain how the de Broglie’s hypothesis gives the rationale for the quantization of angular momentum in Bohr’s quantum theory of the hydrogen atom
Describe the Davisson–Germer experiment
Interpret de Broglie’s idea of matter waves and how they account for electron diffraction phenomena

$\lambda .$

and the rest mass energy is

${E}_{0}={m}_{0}{c}^{2}=\left(0.65\text{kg}\right){\left(2.998\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\text{m/s}\right)}^{2}=5.84\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{16}\text{J.}$

Significance We see from these estimates that De Broglie’s wavelengths of macroscopic objects such as a ball are immeasurably small. Therefore, even if they exist, they are not detectable and do not affect the motion of macroscopic objects.

Check Your Understanding What is de Broglie’s wavelength of a nonrelativistic proton with a kinetic energy of 1.0 eV?

$\lambda \phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}2$

This equation is the first of Bohr’s quantization conditions, given by (Figure) . Providing a physical explanation for Bohr’s quantization condition is a convincing theoretical argument for the existence of matter waves.

The Electron Wave in the Ground State of Hydrogen Find the de Broglie wavelength of an electron in the ground state of hydrogen.

Significance We obtain the same result when we use (Figure) directly.

Check Your Understanding Find the de Broglie wavelength of an electron in the third excited state of hydrogen.

$\lambda =2\pi n{a}_{0}=2\text{(}3.324\phantom{\rule{0.2em}{0ex}}\text{Å}\text{)}=6.648\phantom{\rule{0.2em}{0ex}}\text{Å}$

$\text{Δ}V,$

Diffraction lines measured with low-energy electrons, such as those used in the Davisson–Germer experiment, are quite broad (see (Figure) ) because the incident electrons are scattered only from the surface. The resolution of diffraction images greatly improves when a higher-energy electron beam passes through a thin metal foil. This occurs because the diffraction image is created by scattering off many crystalline planes inside the volume, and the maxima produced in scattering at Bragg angles are sharp (see (Figure) ).

Neutron Scattering Suppose that a neutron beam is used in a diffraction experiment on a typical crystalline solid. Estimate the kinetic energy of a neutron (in eV) in the neutron beam and compare it with kinetic energy of an ideal gas in equilibrium at room temperature.

${E}_{T}$

Kinetic energy of ideal gas in equilibrium at 300 K is:

${K}_{T}=\frac{3}{2}{k}_{B}T=\frac{3}{2}\left(8.62\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-5}\text{eV}\phantom{\rule{0.1em}{0ex}}\text{/}\phantom{\rule{0.1em}{0ex}}\text{K}\right)\left(300\text{K}\right)=38.8\phantom{\rule{0.2em}{0ex}}\text{MeV}.$

We see that these energies are of the same order of magnitude.

Significance Neutrons with energies in this range, which is typical for an ideal gas at room temperature, are called “thermal neutrons.”

Wavelength of a Relativistic Proton In a supercollider at CERN, protons can be accelerated to velocities of 0.75 c . What are their de Broglie wavelengths at this speed? What are their kinetic energies?

${E}_{0}={m}_{0}{c}^{2}=\left(1.672\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{-27}\text{kg}\right){\left(2.998\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{8}\text{m/s}\right)}^{2}=938\phantom{\rule{0.2em}{0ex}}\text{MeV}.$

Check Your Understanding Find the de Broglie wavelength and kinetic energy of a free electron that travels at a speed of 0.75 c .

$\lambda =2.14\phantom{\rule{0.2em}{0ex}}\text{pm;}$

De Broglie’s hypothesis of matter waves postulates that any particle of matter that has linear momentum is also a wave. The wavelength of a matter wave associated with a particle is inversely proportional to the magnitude of the particle’s linear momentum. The speed of the matter wave is the speed of the particle.
De Broglie’s concept of the electron matter wave provides a rationale for the quantization of the electron’s angular momentum in Bohr’s model of the hydrogen atom.
In the Davisson–Germer experiment, electrons are scattered off a crystalline nickel surface. Diffraction patterns of electron matter waves are observed. They are the evidence for the existence of matter waves. Matter waves are observed in diffraction experiments with various particles.

Conceptual Questions

Which type of radiation is most suitable for the observation of diffraction patterns on crystalline solids; radio waves, visible light, or X-rays? Explain.

X-rays, best resolving power

$\text{γ}\text{-rays}$

If an electron and a proton are traveling at the same speed, which one has the shorter de Broglie wavelength?

If a particle is accelerating, how does this affect its de Broglie wavelength?

Why is the wave-like nature of matter not observed every day for macroscopic objects?

negligibly small de Broglie’s wavelengths

What is the wavelength of a neutron at rest? Explain.

Why does the setup of Davisson–Germer experiment need to be enclosed in a vacuum chamber? Discuss what result you expect when the chamber is not evacuated.

to avoid collisions with air molecules

At what velocity will an electron have a wavelength of 1.00 m?

$5.0\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{6}\text{m/s}$

What is the de Broglie wavelength of an electron that is accelerated from rest through a potential difference of 20 keV?

What is the de Broglie wavelength of a proton whose kinetic energy is 2.0 MeV? 10.0 MeV?

20 fm; 9 fm

What is the de Broglie wavelength of a 10-kg football player running at a speed of 8.0 m/s?

(a) What is the energy of an electron whose de Broglie wavelength is that of a photon of yellow light with wavelength 590 nm? (b) What is the de Broglie wavelength of an electron whose energy is that of the photon of yellow light?

a. 2.103 eV; b. 0.846 nm

The de Broglie wavelength of a neutron is 0.01 nm. What is the speed and energy of this neutron?

What is the wavelength of an electron that is moving at a 3% of the speed of light?

At what velocity does a proton have a 6.0-fm wavelength (about the size of a nucleus)? Give your answer in units of c .

What is the velocity of a 0.400-kg billiard ball if its wavelength is 7.50 fm?

$2.21\phantom{\rule{0.2em}{0ex}}×\phantom{\rule{0.2em}{0ex}}{10}^{\text{−}19}\text{m/s}$

Share This Book

Sciencing_Icons_Science SCIENCE

Sciencing_icons_biology biology, sciencing_icons_cells cells, sciencing_icons_molecular molecular, sciencing_icons_microorganisms microorganisms, sciencing_icons_genetics genetics, sciencing_icons_human body human body, sciencing_icons_ecology ecology, sciencing_icons_chemistry chemistry, sciencing_icons_atomic & molecular structure atomic & molecular structure, sciencing_icons_bonds bonds, sciencing_icons_reactions reactions, sciencing_icons_stoichiometry stoichiometry, sciencing_icons_solutions solutions, sciencing_icons_acids & bases acids & bases, sciencing_icons_thermodynamics thermodynamics, sciencing_icons_organic chemistry organic chemistry, sciencing_icons_physics physics, sciencing_icons_fundamentals-physics fundamentals, sciencing_icons_electronics electronics, sciencing_icons_waves waves, sciencing_icons_energy energy, sciencing_icons_fluid fluid, sciencing_icons_astronomy astronomy, sciencing_icons_geology geology, sciencing_icons_fundamentals-geology fundamentals, sciencing_icons_minerals & rocks minerals & rocks, sciencing_icons_earth scructure earth structure, sciencing_icons_fossils fossils, sciencing_icons_natural disasters natural disasters, sciencing_icons_nature nature, sciencing_icons_ecosystems ecosystems, sciencing_icons_environment environment, sciencing_icons_insects insects, sciencing_icons_plants & mushrooms plants & mushrooms, sciencing_icons_animals animals, sciencing_icons_math math, sciencing_icons_arithmetic arithmetic, sciencing_icons_addition & subtraction addition & subtraction, sciencing_icons_multiplication & division multiplication & division, sciencing_icons_decimals decimals, sciencing_icons_fractions fractions, sciencing_icons_conversions conversions, sciencing_icons_algebra algebra, sciencing_icons_working with units working with units, sciencing_icons_equations & expressions equations & expressions, sciencing_icons_ratios & proportions ratios & proportions, sciencing_icons_inequalities inequalities, sciencing_icons_exponents & logarithms exponents & logarithms, sciencing_icons_factorization factorization, sciencing_icons_functions functions, sciencing_icons_linear equations linear equations, sciencing_icons_graphs graphs, sciencing_icons_quadratics quadratics, sciencing_icons_polynomials polynomials, sciencing_icons_geometry geometry, sciencing_icons_fundamentals-geometry fundamentals, sciencing_icons_cartesian cartesian, sciencing_icons_circles circles, sciencing_icons_solids solids, sciencing_icons_trigonometry trigonometry, sciencing_icons_probability-statistics probability & statistics, sciencing_icons_mean-median-mode mean/median/mode, sciencing_icons_independent-dependent variables independent/dependent variables, sciencing_icons_deviation deviation, sciencing_icons_correlation correlation, sciencing_icons_sampling sampling, sciencing_icons_distributions distributions, sciencing_icons_probability probability, sciencing_icons_calculus calculus, sciencing_icons_differentiation-integration differentiation/integration, sciencing_icons_application application, sciencing_icons_projects projects, sciencing_icons_news news.

Share Tweet Email Print
Home ⋅
Science ⋅

De Broglie Wavelength: Definition, Equation & How to Calculate

French physicist Louis de Broglie won the Nobel Prize in 1929 for groundbreaking work in quantum mechanics. His work to show mathematically how subatomic particles share some wave properties was later proven correct through experiment.

Wave-Particle Duality

Particles that exhibit both wave and particle properties are said to have wave-particle duality . This natural phenomenon was first observed in electromagnetic radiation, or light, which can be described as either an electromagnetic wave or a particle known as the photon.

When acting as a wave, light follows the same rules as other waves in nature. For example, in a double-slit experiment, the resulting patterns of wave interference show light's wave nature.

In other situations, light exhibits particle-like behavior, such as when observing the photoelectric effect or Compton scattering. In these cases, photons appear to move in discrete packets of kinetic energy following the same rules of motion as any other particle (although photons are massless).

Matter Waves and the de Broglie Hypothesis

The de Broglie hypothesis is the idea that matter (anything with mass) can also exhibit wavelike properties. Moreover, these resulting matter waves are central to a quantum mechanical understanding of the world – without them, scientists would not be able to describe nature on its smallest scale.

Thus, the wave nature of matter is most noticeable in quantum theory, for example when studying the behavior of electrons. De Broglie was able to mathematically determine what the wavelength of an electron should be by connecting Albert Einstein's mass-energy equivalency equation (E = mc 2 ) with Planck's equation (E = hf), the wave speed equation (v = λf ) and momentum in a series of substitutions.

Setting the first two equations equal to one another under the assumption that particles and their wave forms would have equal energies:

(where E is energy, m is mass and c is the speed of light in a vacuum, h is the Planck constant and f is frequency).

Then, because massive particles do not travel at the speed of light, replacing c with the velocity of the particle v :

Next replacing f with v/λ (from the wave speed equation, where λ [lambda] is wavelength), and simplifying:

Finally, because momentum p is equal to mass m times velocity v:

This is known as the de Broglie equation. As with any wavelength, standard unit of measure for the de Broglie wavelength is meters (m).

de Broglie Wavelength Calculations

The wavelength for a particle of momentum p is given by: λ = h/p

where λ is wavelength in meters (m), h is Planck's constant in joule-seconds (6.63 × 10 -34 Js) and p is momentum in kilogram-meters per second (kgm/s).

Example: What is the de Broglie wavelength of 9.1 × 10 -31 × 10 6 m/s?

Note that for very large masses – meaning something on the scale of everyday objects, like a baseball or a car – this wavelength becomes vanishingly small. In other words, the de Broglie wavelength doesn't have much impact on the behavior of objects we can observe unaided; it isn't needed to determine where a baseball pitch will land or how much force it takes to push a car down the road. The de Broglie wavelength of an electron, however, is a significant value in describing what electrons do, since the rest mass of an electron is small enough to put it on the quantum scale.

How to calculate the momentum of a photon of yellow..., the famous physicist who discovered photons, how to calculate energy with wavelength, the modern theory of light, what is planck's constant, do photons have mass, what are the properties of protons, who discovered the particle theory, what is light measured in, can we see light emitted by hydrogen atoms when they..., how to convert nanometers to joules, how to calculate hertz to joules, how to convert photons to joules, how to figure the energy of one mole of a photon.

Chemistry LibreTexts: Deriving the de Broglie Wavelength
Encyclopaedia Britannica: Louis de Broglie

About the Author

Amy Dusto is a high school science teacher and a freelance writer. She holds a Bachelor of Arts in Natural Sciences area and a Master of Arts in Science Writing from Johns Hopkins University. She has contributed to Discovery.com, Climate.gov, Science News and Symmetry Magazine, among other outlets.

Find Your Next Great Science Fair Project! GO

Why Does Water Expand When It Freezes
Gold Foil Experiment
Faraday Cage
Oil Drop Experiment
Magnetic Monopole
Why Do Fireflies Light Up
Types of Blood Cells With Their Structure, and Functions
The Main Parts of a Plant With Their Functions
Parts of a Flower With Their Structure and Functions
Parts of a Leaf With Their Structure and Functions
Why Does Ice Float on Water
Why Does Oil Float on Water
How Do Clouds Form
What Causes Lightning
How are Diamonds Made
Types of Meteorites
Types of Volcanoes
Types of Rocks

de Broglie Wavelength

The de Broglie wavelength is a fundamental concept in quantum mechanics that profoundly explains particle behavior at the quantum level. According to de Broglie hypothesis, particles like electrons, atoms, and molecules exhibit wave-like and particle-like properties.

This concept was introduced by French physicist Louis de Broglie in his doctoral thesis in 1924, revolutionizing our understanding of the nature of matter.

de Broglie Equation

A fundamental equation core to de Broglie hypothesis establishes the relationship between a particle’s wavelength and momentum . This equation is the cornerstone of quantum mechanics and sheds light on the wave-particle duality of matter. It revolutionizes our understanding of the behavior of particles at the quantum level. Here are some of the critical components of the de Broglie wavelength equation:

1. Planck’s Constant (h)

Central to this equation is Planck’s constant , denoted as “h.” Planck’s constant is a fundamental constant of nature, representing the smallest discrete unit of energy in quantum physics. Its value is approximately 6.626 x 10 -34 Jˑs. Planck’s constant relates the momentum of a particle to its corresponding wavelength, bridging the gap between classical and quantum physics.

2. Particle Momentum (p)

The second critical component of the equation is the particle’s momentum, denoted as “p”. Momentum is a fundamental property of particles in classical physics, defined as the product of an object’s mass (m) and its velocity (v). In quantum mechanics, however, momentum takes on a slightly different form. It is the product of the particle’s mass and its velocity, adjusted by the de Broglie wavelength.

The mathematical formulation of de Broglie wavelength is

We can replace the momentum by p = mv to obtain

The SI unit of wavelength is meter or m. Another commonly used unit is nanometer or nm.

This equation tells us that the wavelength of a particle is inversely proportional to its mass and velocity. In other words, as the mass of a particle increases or its velocity decreases, its de Broglie wavelength becomes shorter, and it behaves more like a classical particle. Conversely, as the mass decreases or velocity increases, the wavelength becomes longer, and the particle exhibits wave-like behavior. To grasp the significance of this equation, let us consider the example of an electron .

de Broglie Wavelength of Electron

Electrons are incredibly tiny and possess a minimal mass. As a result, when they are accelerated, such as when they move around the nucleus of an atom , their velocities can become significant fractions of the speed of light, typically ~1%.

Consider an electron moving at 2 x 10 6 m/s. The rest mass of an electron is 9.1 x 10 -31 kg. Therefore,

These short wavelengths are in the range of the sizes of atoms and molecules, which explains why electrons can exhibit wave-like interference patterns when interacting with matter, a phenomenon famously observed in the double-slit experiment.

Thermal de Broglie Wavelength

The thermal de Broglie wavelength is a concept that emerges when considering particles in a thermally agitated environment, typically at finite temperatures. In classical physics, particles in a gas undergo collision like billiard balls. However, particles exhibit wave-like behavior at the quantum level, including wave interference phenomenon. The thermal de Broglie wavelength considers the kinetic energy associated with particles due to their thermal motion.

At finite temperatures, particles within a system possess a range of energies described by the Maxwell-Boltzmann distribution. Some particles have relatively high energies, while others have low energies. The thermal de Broglie wavelength accounts for this distribution of kinetic energies. It helps to understand the statistical behavior of particles within a thermal ensemble.

Mathematical Expression

The thermal de Broglie wavelength (λ th ) is determined by incorporating both the mass (m) of the particle and its thermal kinetic energy (kT) into the de Broglie wavelength equation:

Here, k is the Boltzmann constant, and T is the temperature in Kelvin.

de Broglie Wave Equation – Chem.libretexts.org
de Broglie Wavelength – Spark.iop.org
de Broglie Matter Waves – Openstax.org
Wave Nature of Electron – Hyperphysics.phy-astr.gsu.edu

Article was last reviewed on Friday, October 6, 2023

Join our Newsletter

Fill your E-mail Address

Related Worksheets

Reflection of Light
Equations of Motion
Wave Theory
Electromagnetic Induction
Physics Notes Class 12
Physics Notes Class 8
Physics Notes Class 9
Physics Notes Class 10
Physics Notes Class 11
Angular Momentum
Diagram of Electron Microscope
Torque and Angular Momentum
Angular PrimeNG TabMenu Default
Angular PrimeNG Tag Icons
Angular PrimeNG ScrollTop Element
Angular PrimeNG Tree Icons
Angular PrimeNG Speed Dial Direction
Angular PrimeNG Tree Selection
Moment of Inertia
Angular PrimeNG Button Icons Component
Angular PrimeNG Avatar Icon
Angular PrimeNG Galleria Thumbnail
Electronic Configuration of First 30 Elements
Angular PrimeNG Skeleton Component
Angular PrimeNG Button Basic Component
Angular PrimeNG Tree Loading Status
Angular PrimeNG MegaMenu Horizontal
Angular PrimeNG Chip Icon
Angular PrimeNG Button Badges Component
Integrate Angular 7 with ElectronJS
Angular PrimeNG Button Component
Angular PrimeNG tag Component
Angular PrimeNG Card Component
Angular PrimeNG MegaMenu Component
Angular PrimeNG Badge Component
Angular PrimeNG Toolbar Component
Angular PrimeNG Rating Component
Angular PrimeNG ScrollTop Component

Angular Momentum of Electron

In the world of physics, angular momentum helps us understand how objects behave when they rotate. It is not only limited to big objects like planets but it also helps us gain insight into the motion of smaller particles such as electrons. Let’s understand angular momentum of an electron with the basic introduction of momentum in this article.

What is Angular Momentum ?

Momentum is a physical quantity that an object might possess by virtue of its motion. Angular momentum is when the motion is rotational. Angular momentum is defined as

“The quantity of rotation of a body, which is the product of its moment of inertia and its angular velocity.”

In simpler terms, angular momentum measures how much motion an object has while it’s spinning around a point. The greater the mass of the object and the faster it spins, the more angular momentum it has.

Momentum of an Electron

Bohr put forward a theory about the rotational energy of an electron inside the atom. In Bohr’s atomic model , electrons are positioned in specific paths around the nucleus, and these paths play a crucial role in defining the electron’s angular momentum. Bohr proposed that the orbital angular momentum of an electron is quantized, meaning it can only be found in certain fixed values.

Bohr also specified that the angular momentum of an electron must be a multiple of h/2π, where h is Planck’s constant. This limitation confines electrons to specific stable paths around the nucleus.

Angular Momentum of an Electron

Understanding the chemical properties of elements and the structure of atoms depends significantly on the electron’s angular momentum. It describes the reasons behind atoms absorbing or releasing light at specific wavelengths and why some elements exhibit specific chemical reactions. This knowledge forms the basis for areas such as chemistry, physics, and also materials science.

De Broglie’s Explanation to the Quantization of Angular Momentum of Electron

Expanding on Bohr’s research, Louis de Broglie later proposed the concept that electrons exhibit characteristics of both particles and waves during motion. This duality was a crucial development in comprehending how electrons behave on a quantum scale.

De Broglie applied his hypothesis to the Bohr model of the atom. he said that if electrons behave like waves, then for an electron to exist in a stable orbit around the nucleus, the circumference of its orbit must accommodate an integer number of wavelengths.

This can be shown by this formula, 2πr=nλ. Here, if we substitute λ by h /p where p = mv, we get

and if we use the formula of angular momentum L = mvr and rearrange the expression we get,

In terms of mathematics, the formula for the angular momentum of an electron can be expressed as:

The angular momentum is equal to the product of mass, velocity, and radius, which is also equivalent to half of the reduced Planck constant divided by 2 times pi. L = mvr = n h /2π

Angular momentum is represented by L.
The mass of the electron is denoted by m.
v represents the speed at which the electron is moving.
r represents the size of the orbit.
n is the main quantum number that indicates the orbit in which the electron can be found.
Planck’s constant is denoted by h .

This equation also serves as a foundational principle for contemporary comprehension of atomic structure.

Orbital Angular Momentum

If we use the right formula we can also obtain the Orbital Angular momentum of an electron. As we have already learned that angular momentum is quantized so to make things simpler here we make use of orbital quantum number ‘l’ instead of ‘n’. The formula is given as :

L = √l(l+1) h

This makes it easier to calculate the orbital angular momentum of any orbit in an atom. Let’s go through some examples and find orbital angular momentum of p and d electrons.

Orbital Angular Momentum of p-electron

In an atom, electrons are present in different shells and each shell is divided into subshells named s,p,d and f, based on the shape of the orbital in which electrons move. The quantum number of p orbital is ‘1’. So using the formula we learned before and putting l = 1 we get,

L = √1(1+1)h = √2h

This is the magnitude of the angular momentum of an electron in p orbital.

Orbital Angular Momentum of d-electron

In case for d orbital, we have quantum number ‘l’ = ‘2’. Now using the same formula for orbital angular momentum, L = √l(l+1)h we get,

L = √2(2+1)h = √6h

As we can clearly observe this value is higher than that of p- electrons which reflects the more complex spatial arrangement and higher angular momentum associated with d-electrons.

Spin Angular Momentum

Spin angular momentum is an intrinsic property. For easy understanding you can say that electrons have two options for spinning: they can either spin in an “up” direction or in a “down” direction. This does not indicate they are actually spinning in a physical manner; it is merely a method for scientists to explain their magnetic alignment. Actual spin angular momentum is given by the formula :

[Tex]S = \sqrt{s(s+1)} \times \hbar [/Tex]

Where [Tex]\hbar[/Tex] is reduced plank’s constant and s is quantum spin number.

In the above article, we understood angular momentum and learned how to calculated the angular momentum of an electron. Angular momentum is always quantized and is given as multiple of h/2π. By studying the angular momentum of electrons in different orbitals, such as p and d, scientists can gain deeper insights into the nature of materials and the fundamental forces at play at the atomic level. This understanding will help us in solving question related to angular momentum.

Also, Check

Bohr’s Model of the Hydrogen Atom Dual Nature of Matter Quantum Numbers

FAQs on Angular Momentum of Electron

What is the formula for the orbital angular momentum of an electron.

The orbital angular momentum for an electron revolving in an orbit is given by √l(l+1)h2π.

What is the angular momentum of S?

For s-orbital angular momentum is zero and for a p-orbital angular momentum is non-zero.

What is the de Broglie’s equation?

De Broglie Wavelength for an Electron is given by the equation λ = h/mv.

What is the dual nature of electrons?

The dual nature of electrons is particle nature as well as wave nature was established by this equation. The three-dimensional region in space around the nucleus where the probability of finding an electron was killer energy maximum is called an atomic orbital.

What is the value of angular momentum of Bohr orbit?

The angular momentum of an electron in a Bohr orbit of H-atom is 4.2178×10 −34 kgm 2 /sec.

Please Login to comment...

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons
Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

2.1: The de Broglie-Bohr Model for the Hydrogen Atom

Last updated
Save as PDF
Page ID 154844

Frank Rioux
College of Saint Benedict/Saint John's University

$ \lambda = \frac{h}{mv}$ de Broglie's hypothesis that matter has wave-like properties.

$n \lambda = 2 \pi r$ The consequence of de Broglie's hypothesis; an integral number of wavelengths must fit within the circumference of the orbit. This introduces the quantum number which can have values 1, 2, 3...

$mv = \frac{nh}{2 \pi r}$ Substitution of the first equation into the second equation reveals that linear momentum is quantized.

$ T = \frac{1}{2} mv^2 = \frac{n^2 h^2}{8 \pi^2 m_e r^2}$ If momentum is quantized, so it kinetic energy.

$E = T + V = \frac{n^2 h^2}{8 \pi^2 m_e r^2} - \frac{e^2}{4 \pi \varepsilon_0 r}$ Which means that total energy is quantized.

Below the ground state energy and orbit radius of the electron in the hydrogen atom is found by plotting the energy as a function of the orbital radius. The ground state is the minimum in the curve.

Fundamental constants: electron charge, electron mass, Planck's constant, vacuum permitivity.

\[ \begin{matrix} e = 1.6021777 (10)^{-19} \text{coul} & m_e= 9.10939 (10)^{-31} \text{kg} \\ h = 6.62608 (10)^{-34} \text{joule sec} & \varepsilon_0 = 8.85419 (10)^{-12} \frac{ \text{coul}^2}{ \text{joule m}} \end{matrix} \nonumber \]

Quantum number and conversion factor between meters and picometers and joules and atto joules.

\[ \begin{matrix} n = 1 & pm = 10^{-12} m & \text{ajoule} = 10^{-18} \text{joule} \end{matrix} \nonumber \]

\[ \begin{matrix} r = 20 pm,~20.5 pm .. 500 pm & T(r) = \frac{n^2 h^2}{8 \pi^2 m_e r^2} & V(r) = - \frac{e^2}{4 \pi \varepsilon_0 r} & E(r) = T(r) + V(r) \end{matrix} \nonumber \]

Screen Shot 2019-06-04 at 6.00.26 PM.png

This figure shows that atomic stability involves a balance between potential and kinetic energy. The electron is drawn toward the nucleus by the attractive potential energy interaction (~ ‐1/R), but is prevented from spiraling into the nucleus by the extremely large kinetic energy (~1/R2) associated with small orbits.

Prepared by Frank Rioux.

IMAGES

de Broglie equation, derivation, and its Significance
De Broglie Hypothesis
de Broglie Equation
de Broglie equation
De Broglie Equation
DE BROGLIE HYPOTHESIS Presentation

VIDEO

De Broglie Hypothesis
13 Modern Physics
Davisson
de Broglie Hypothesis
DE BROGLIE HYPOTHESIS || DUAL NATURE OF MATTER|| CLASS 12 CBSE, JEE, NEET
de Broglie Hypothesis in Urdu/Hindi by Prof. Ahmad Saeed

COMMENTS

6.6: De Broglie's Matter Waves
Compton's formula established that an electromagnetic wave can behave like a particle of light when interacting with matter. In 1924, Louis de Broglie proposed a new speculative hypothesis that electrons and other particles of matter can behave like waves. Today, this idea is known as de Broglie's hypothesis of matter waves.In 1926, De Broglie's hypothesis, together with Bohr's early ...
Matter wave
Matter waves are a central part of the theory of quantum mechanics, being half of wave-particle duality.At all scales where measurements have been practical, matter exhibits wave-like behavior.For example, a beam of electrons can be diffracted just like a beam of light or a water wave.. The concept that matter behaves like a wave was proposed by French physicist Louis de Broglie (/ d ə ˈ b ...
de Broglie Wavelength
The thermal de Broglie wavelength (λ th) is approximately the average de Broglie wavelength of the gas particles in an ideal gas at the specified temperature. The thermal de Broglie wavelength is given by the expression: λ D = h / √ 2 π m k B T. where, h = Planck constant. m = mass of a gas particle.
6.5 De Broglie's Matter Waves
Compton's formula established that an electromagnetic wave can behave like a particle of light when interacting with matter. In 1924, Louis de Broglie proposed a new speculative hypothesis that electrons and other particles of matter can behave like waves. Today, this idea is known as de Broglie's hypothesis of matter waves.In 1926, De Broglie's hypothesis, together with Bohr's early ...
Deriving the de Broglie Wavelength
In 1923, Louis de Broglie, a French physicist, proposed a hypothesis to explain the theory of the atomic structure. By using a series of substitution de Broglie hypothesizes particles to hold properties of waves. Within a few years, de Broglie's hypothesis was tested by scientists shooting electrons and rays of lights through slits.
De Broglie Hypothesis
De Broglie successfully provided the explanation to Bohr's assumption by his hypothesis. Today we know that every particle exhibits both matter and wave nature. This is called wave-particle duality. The concept that matter behaves like wave is called the de Broglie hypothesis, named after Louis de Broglie, who proposed it in 1924.
De Broglie Hypothesis
To calculate the De Broglie wavelength of an electron, we use the formula derived by Louis de Broglie which relates a particle's wavelength to its momentum. The formula is: 𝜆 = ℎ/𝑝 where: 𝜆 is the wavelength, ℎ is Planck's constant, approximately 6.626×10⁻³⁴ Joule seconds, 𝑝 is the momentum of the electron.
De-Broglie Wavelength Formula: Equations, Solved Examples
The de Broglie wavelength of the photon can be computed using the formula: λ = h p. = 6.62607 × 10 − 34 Js 1.50 × 10 − 27 kgm / s. = 4.42 × 10 − 7 m. = 442 × 10 − 9 m. = 442 nm. The de Broglie wavelength of the photon will be 442 nm, and this wavelength lies in the blue-violet part of the visible light spectrum. Q.2.
What Is the De Broglie Equation?
The de Broglie equation is an equation used to describe the wave properties of matter, specifically, the wave nature of the electron : . λ = h/mv, where λ is wavelength, h is Planck's constant, m is the mass of a particle, moving at a velocity v. de Broglie suggested that particles can exhibit properties of waves.
18.2: Quantized Energy
De Broglie's hypothesis is an independent postulate about the structure of nature. In this respect, its status is the same as that of Newton's laws or the laws of thermodynamics. Nonetheless, we can construct a line of thought that is probably similar to de Broglie's, recognizing that these are heuristic arguments and not logical ...
de Broglie Equation
This equation relating the momentum of a particle with its wavelength is the de Broglie equation, and the wavelength calculated using this relation is the de Broglie wavelength. Relation between de Broglie Equation and Bohr's Hypothesis of Atom. Bohr postulated that the angular momentum of an electron revolving around the nucleus is quantized ...
De Broglie Wavelength Hypothesis Overview
The De Broglie hypothesis proposes that all matter exhibits wave-like properties and relates the observed wavelength of matter to its momentum. After Albert Einstein's photon theory became accepted, the question became whether this was true only for light or whether material objects also exhibited wave-like behavior. Here is how the De Broglie hypothesis was developed.
De Broglie Equation
While this equation was specifically for waves, de Broglie, using his hypothesis that particles can act like waves, combined the equations: E = m c 2 = h ν. Where E is energy, m is mass, c is the ...
What is De Broglie Hypothesis?
De Broglie's Hypothesis says that Matter consists of both the particle nature as well as wave nature. De Broglie wavelength λ is given as λ = h p, where p represents the particle momentum and can be written as: λ = h m v Where, h is the Planck's constant, m is the mass of the particle, and v is the velocity of the particle.; From the above relation, it can be said that the wavelength of the ...
Louis de Broglie
Louis Victor Pierre Raymond, 7th Duc de Broglie (/ d ə ˈ b r oʊ ɡ l i /, also US: / d ə b r oʊ ˈ ɡ l iː, d ə ˈ b r ɔɪ /, French: [də bʁɔj] or [də bʁœj] ⓘ; 15 August 1892 - 19 March 1987) was a French aristocrat and physicist who made groundbreaking contributions to quantum theory.In his 1924 PhD thesis, he postulated the wave nature of electrons and suggested that all ...
De Broglie Equation
The wavelength is known as the de Broglie wavelength. For an electron, de Broglie wavelength equation is: λ =. h mv h m v. Here, λ points to the wave of the electron in question. M is the mass of the electron. V is the velocity of the electron. Mv is the momentum that is formed as a result.
De Broglie's Matter Waves
Compton's formula established that an electromagnetic wave can behave like a particle of light when interacting with matter. In 1924, Louis de Broglie proposed a new speculative hypothesis that electrons and other particles of matter can behave like waves. Today, this idea is known as de Broglie's hypothesis of matter waves.In 1926, De Broglie's hypothesis, together with Bohr's early ...
11.5: de Broglie's Postulate
To calculate the de Broglie wavelength (Equation 11.5.1 ), the momentum of the particle must be established and requires knowledge of both the mass and velocity of the particle. The mass of an electron is 9.109383 × 10 − 28 g and the velocity is obtained from the given kinetic energy of 1000 eV: KE = mv2 2 = p2 2m = 1000 eV.
De Broglie Wavelength: Definition, Equation & How to Calculate
De Broglie was able to mathematically determine what the wavelength of an electron should be by connecting Albert Einstein's mass-energy equivalency equation (E = mc 2) with Planck's equation (E = hf), the wave speed equation (v = λf ) and momentum in a series of substitutions. Setting the first two equations equal to one another under the ...
de Broglie Wavelength: Definition, Hypothesis, and Equation
A fundamental equation core to de Broglie hypothesis establishes the relationship between a particle's wavelength and momentum.This equation is the cornerstone of quantum mechanics and sheds light on the wave-particle duality of matter. It revolutionizes our understanding of the behavior of particles at the quantum level.
Wave nature of electron
DeBroglie Hypothesis Suggested by De Broglie in about 1923, the path to the wavelength expression for a particle is by analogy to the momentum of a photon. ... When you have finished entering data, click on the quantity you wish to calculate in the formula above. Wavelength values will be reconciled, but no further calculation will be done ...
Angular Momentum of Electron: Definition, Formula, De-Broglie's
De Broglie applied his hypothesis to the Bohr model of the atom. he said that if electrons behave like waves, then for an electron to exist in a stable orbit around the nucleus, the circumference of its orbit must accommodate an integer number of wavelengths. This can be shown by this formula, 2πr=nλ.
2.5: The de Broglie-Bohr Model for the Hydrogen Atom
The de Broglie‐Bohr model of the hydrogen atom presented here treats the electron as a particle on a ring with wave‐like properties. λ = h mev λ = h m e v. de Broglie's hypothesis that matter has wave-like properties. nλ = 2πr n λ = 2 π r. The consequence of de Broglieʹs hypothesis; an integral number of wavelengths must fit within ...
2.1: The de Broglie-Bohr Model for the Hydrogen Atom
λ = h mv λ = h m v de Broglie's hypothesis that matter has wave-like properties. nλ = 2πr n λ = 2 π r The consequence of de Broglie's hypothesis; an integral number of wavelengths must fit within the circumference of the orbit. This introduces the quantum number which can have values 1, 2, 3... mv = nh 2πr m v = n h 2 π r Substitution ...

6.6: De Broglie’s Matter Waves

Learning Objectives

Example \(\PageIndex{1}\): How Long are de Broglie Matter Waves?

Exercise \(\PageIndex{1}\)

Example \(\PageIndex{2}\): The Electron Wave in the Ground State of Hydrogen

Exercise \(\PageIndex{2}\)

Example \(\PageIndex{3A}\): Neutron Scattering

Example \(\PageIndex{3B}\): Wavelength of a Relativistic Proton

Exercise \(\PageIndex{3}\)

6.5 De Broglie’s Matter Waves

Example 6.11

Significance

Example 6.12

Example 6.13

Example 6.14

De Broglie Hypothesis

De Broglie Equation

De Broglie Hypothesis

De Broglie Equation Derivation

Step 1: Relating Energy and Momentum for Light

Step 2: Applying the Concept to Material Particles

Step 3: De Broglie Wavelength of Particles

De Broglie Wavelength for an Electron

Calculating Momentum

Significance of the De Broglie Equation

Fundamental to Quantum Mechanics

Basis for Modern Physics Theories

Experimental Validation and Applications

Technological Impact

Educational and Conceptual Influence

Relation between De Broglie Equation and Bohr’s Hypothesis of Atom

Bohr’s Hypothesis of the Atom

Integrating De Broglie’s Equation with Bohr’s Model

Substituting De Broglie’s Equation

Examples of De Broglie Hypothesis

Electron Diffraction

Scanning Tunneling Microscope (STM)

Bohr Model of the Atom

Matter Waves

Neutron Interferometry

Atomic Force Microscopy (AFM)

How was the De Broglie Equation derived?

Why is the De Broglie Equation important?

Can the De Broglie Equation be applied to all objects?

What is wave-particle duality?

AI Generator

De Broglie Hypothesis

De Broglie's Thesis

Alternate Formulations

Experimental Confirmation

Significance of the de Broglie Hypothesis

Macroscopic Objects and Wavelength

What is De Broglie Hypothesis?

Introduction

What is the De Broglie Equation?

Significance of De Broglie Equation

De Broglie Wavelength for an Electron

The Conclusion of De Broglie Hypothesis

FAQs on De Broglie Equation

De Broglie’s Matter Waves

Learning Objectives

Conceptual Questions

Share This Book

Sciencing_Icons_Science SCIENCE

De Broglie Wavelength: Definition, Equation & How to Calculate

Wave-Particle Duality

Matter Waves and the de Broglie Hypothesis

de Broglie Wavelength Calculations

Related Articles

Find Your Next Great Science Fair Project! GO

de Broglie Wavelength

de Broglie Equation

1. Planck’s Constant (h)

2. Particle Momentum (p)

de Broglie Wavelength of Electron

Thermal de Broglie Wavelength

Mathematical Expression

Related articles

Leave a Reply Cancel reply

Popular Articles